Rearuh

  關於本条目的避免深奥术语且更容易理解的版本，請見“量子力学入门”。

1927年第五次索尔维会议，此次會議主題為「電子和光子」，世界上最主要的物理學家聚集在一起討論新近表述的量子理論。

量子力学（英語：quantum mechanics）是物理學的分支學科。它主要描写微观的事物，与相对论一起被认为是现代物理学的两大基本支柱，许多物理学理论和科学，如原子物理学、固体物理学、核物理学和粒子物理学以及其它相关的學科，都是以其为基础。

19世紀末，人們發現舊有的經典理論無法解釋微观系统，於是經由物理學家的努力，在20世紀初創立量子力学，解釋了這些現象。量子力學從根本上改變人類對物質結構及其相互作用的理解。除了透过广义相对论描写的引力外，迄今所有基本相互作用均可以在量子力学的框架内描述（量子场论）。

愛因斯坦可能是在科學文獻中最先給出術語「量子力學」的物理學者。^[1]:86[a]

关键现象、歷史背景

黑体辐射

普朗克定律（绿）、維恩定律（蓝）和瑞利-金斯定律（红）在频域下的比较，可见维恩定律在高频区域和普朗克定律相符，瑞利-金斯定律在低频区域和普朗克定律相符。

理想黑体可以吸收所有照射到它表面的電磁辐射，并将这些辐射转化为热辐射，其光谱特征仅与该黑体的温度有关，與黑體的材質無關。从古典物理学出发推導出的維恩定律在低頻區域與實驗數據不相符，而在高頻區域，从古典物理学的能量均分定理推導出瑞利-金斯定律又與實驗數據不相符，在辐射频率趋向无穷大时，能量也會變得無窮大，這結果被称作“紫外灾变”。然而在那時，普朗克並未注意到紫外灾变的嚴重性。

1900年12月4日，後來被定為量子力學的誕辰，马克斯·普朗克在柏林科學院發表報告，通過將維恩定律加以改良，又將波茲曼熵公式重新詮釋，他得出了一个与实验数据完全吻合的普朗克公式来描述黑体辐射，但是在诠释这个公式时，他将在物体裡發射與吸收輻射的原子視為微小的量子谐振子，並且假设这些量子谐振子的能量不是连续的，而是离散的數值，並且單獨量子谐振子吸收和發射的辐射能是量子化的。^{[2]:第2章[1]:58-66[3]:364-372}

光电效应

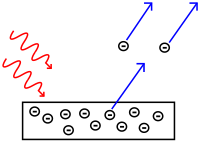
光電效應示意圖：來自左上方的光子衝擊到金屬板，將電子逐出金屬板，並且向右上方移去。

海因里希·赫兹於1887年做实验发现，如果照射紫外光於金属表面，則电子會從金属表面被發射出来，他因此發現了光電效應。1905年，爱因斯坦提出了光量子的理论来解释这个现象。他認為，光束是由一群離散的光量子所組成，而不是連續性波動。這些光量子現今被稱為光子，其能量E{displaystyle E}为

E=hν{displaystyle E=hnu }

这裡，ν{displaystyle nu } 是頻率。

爱因斯坦大膽地預言，假若光子的頻率高於金屬的極限頻率，則這光子可以給予足夠能量來使得金屬表面的一個電子逃逸，造成光電效應。电子获得的能量中，一部分被用来将金属中的电子射出，这部分能量叫逸出功，（用Ew{displaystyle E_{mbox{w}}}表示），另一部分成為了逃逸电子的動能：

hν=Ew+12mv2{displaystyle hnu =E_{mbox{w}}+{frac {1}{2}}mv^{2}}

这裡 m{displaystyle m} 是电子的质量，v{displaystyle v} 是其速度。

假若光的频率低於金屬的極限頻率，那么它无法使得电子获得足够的逸出功。这时，不论輻照度有多大，照射時間有多長，都不會發生光電效應。而当入射光的頻率高於極限頻率時，即使光不夠強，當它射到金屬表面時也會觀察到光電子發射。羅伯特·密立根後來做實驗證明這些理論與預言屬實。

爱因斯坦將普朗克的量子理论加以延伸擴展，他提出不仅仅物质与电磁辐射之间的相互作用是量子化的，而且量子化是一个基本物理特性的理论。通过这个新理论，他得以解释光电效应。^{[4]:1060-1063[1]:67-68}

原子结构

按照氫原子或類氫原子的玻爾模型，帶負價的電子被侷限於原子殼層，它們環繞著尺寸很小的帶正價原子核。電子從一個能量較高的軌道躍遷到能量較低的軌道時，會以電磁波的形式將能量差釋出。^[5]:49-82

20世纪初，卢瑟福模型被公认为正确的原子模型。这个模型假设带负电荷的电子，像行星围绕太阳运转一样，围绕带正电荷的原子核运转。在这个过程中库仑力与离心力必须平衡。

但是这个模型有两个问题无法解决。首先，按照經典电磁学，这个模型不稳定，由於电子不断地在它的运转过程中被加速，它应该會通过發射电磁波丧失能量，这样它很快就会坠入原子核。其次，实验结果显示，原子的发射光谱是由一系列离散的发射线组成，比如氢原子的发射光谱是由一个紫外线系列（來曼系）、一个可见光系列（巴耳麥系）和其它的红外线系列组成；而按照經典理论原子的发射谱应该是连续的。

1913年，尼尔斯·玻尔提出了玻尔模型，这个模型引入量子化的概念來解釋原子结构和光谱线。玻尔认为，电子只能在对应某些特定能量值En{displaystyle E_{n}}的轨道上运動。假如一个电子，从一个能量比较高的轨道（En{displaystyle E_{n}}），躍遷到一个能量比较低的轨道（Em{displaystyle E_{m}}）上时，它发射的光的频率为

ν=En−Emh{displaystyle nu ={frac {E_{n}-E_{m}}{h}}}

反之，通过吸收同样频率的光子，电子可以从低能的轨道，躍遷到高能的轨道上。

玻尔模型可以解释氢原子的结构。改善的玻尔模型，还可以解释類氫原子的結構，即 He⁺, Li²⁺, Be³⁺ 等。但它还不够完善，仍然无法准确地解释其它原子的物理现象。^{[1]:53-57[6]:24-29}

物质波

外村彰（日语：外村彰）（Akira Tonomura）團隊做電子雙縫實驗得到的干涉圖樣：每秒約有1000個電子抵達探測屏，電子與電子之間的距離約為150km，兩個電子同時存在於電子發射器與探測屏之間的概率微乎其微。圖中每一亮點表示一個電子抵達探測屏，^[b]經過一段時間，電子的累積顯示出干涉圖樣。^[8]

1924年，路易·德布罗意發表博士論文提出，粒子拥有波动性，其波长λBroglie{displaystyle lambda _{Broglie}}与动量p{displaystyle p}成反比，以方程式表示為^[9]

λBroglie=hp{displaystyle lambda _{Broglie}={frac {h}{p}}}。

這理論稱為德布羅意假說，又稱為物質波假說。這意味著電子也具有波動性。

1927年，克林顿·戴维森與雷斯特·革末做實驗將低能量電子入射於鎳晶體，然後測量對於每一個角度的散射強度。從分析實驗數據，他們發現，假設加速電勢為5.4eV，則在50°之處會出現強勁反射，符合威廉·布拉格於1913年所提出的 X射線繞射性質。這驚人的結果證實電子是一種物質波，也證實了物質波假說。這實驗就是著名的戴維森－革末實驗。^[6]:64-68

电子的双缝实验可以非常生动地展示出多种不同的量子力学现象。^[10]如右图所示，

• 打在屏幕上的电子是点状的，这个现象与一般感受到的点状的粒子相同。^[b]
  


• 电子打在屏幕上的位置，有一定的分布概率，随时间可以看出双缝衍射所特有的条纹图像。假如一个光缝被关闭的话，所形成的图像是单缝特有的波的分布概率。

在图中的实验裡，电子源的强度非常低，所發射出的電子與電子之間的距離約為150km，任意兩個電子同時存在於電子發射器與探測屏之間的概率微乎其微。显然可以推斷，單獨电子同时通过了两條狹缝，自己與自己發生干涉，从而出現这个干涉圖樣。对于經典物理学来说，这个解释非常奇怪。从量子力学的角度来看，电子的分布概率可以用两个分別通过两條狹縫的量子态疊加在一起來解釋。这个实验非常具有信服力地展示出電子的波動性。^[8]

数学基础

在二十世紀二十年代，出现了两种量子物理的理论，即维尔纳·海森堡的矩阵力学和埃尔温·薛定谔的波动力学。

海森堡主張，只有在實驗裏能夠觀察到的物理量（可觀察量），才具有物理意義，才可以用理論描述其物理行為，例如，不能直接觀察到電子運動於原子裏的位置與週期。因此，他著重於研究電子躍遷時所發射光波的離散頻率和輻照度，這些是可觀察量。但是，他無法實際應用這點子於氫原子問題，因為這問題太過複雜，他只能改應用這點子於比較簡單，但也比較不實際的問題。經過一番努力，他計算出諧振子問題的能譜與零點能量，符合分子光譜學的結果。另外，在海森堡理論中，系統的哈密頓量是位置和動量的函數，但它們不再具有古典力學中的定義，而是由二階（代表著過程的初態和終態）傅立葉係數的矩陣給出。海森堡還發現，這些矩陣互不對易。這些論述後來發展成為矩陣力學。^[1]:161-163

從德布羅意論文的相對論性理論，薛定谔推導出一種波動方程式，稱為薛定谔方程式；用這方程式可以計算出氫原子的譜線，得到與波耳模型完全相同的答案。波动力学的基礎方程式就是薛定谔方程式^[1]:163-164

薛定谔率先於1926年证明了这两种理论的等价性。稍后，卡爾·埃卡特（英语：Carl Eckart）和沃爾夫岡·包立也给出類似证明，^[1]:166约翰·冯·诺伊曼严格地证明了波动力学和矩阵力学的等价性。^[11]

基礎公設

整個量子力学的数学理论可以建立於基礎公設。這些公設不能被嚴格推導出來的，而是從實驗結果仔細分析而得到的。從這幾個公設，可以推導出整個量子力學。假若量子力學的理論結果符合實驗結果，則可以認定這些基礎公設正確無誤，否則，必需加以修正。至今為止，量子力學已被實驗核對至極高準確度，還沒有找到任何與理論不符合的實驗結果，雖然有些理論很難直覺地用經典物理的概念來理解，例如，波粒二象性、量子糾纏等等。^{[12][13]:211ff[14]:165-167}

1. 量子態公設：量子系统在任意时刻的状态（量子態）可以由希尔伯特空间 H{displaystyle {mathcal {H}}} 中的態矢量 |ψ⟩{displaystyle |psi rangle } 来設定，這態矢量完備地給出了這量子系統的所有信息。這公設意味著量子系統遵守态叠加原理，假若|ψ1⟩{displaystyle |psi _{1}rangle }、|ψ2⟩{displaystyle |psi _{2}rangle }屬於希尔伯特空间H{displaystyle {mathcal {H}}}，則c1|ψ1⟩+c2|ψ2⟩{displaystyle c_{1}|psi _{1}rangle +c_{2}|psi _{2}rangle }也屬於希尔伯特空间H{displaystyle {mathcal {H}}}。


2. 時間演化公設： 态矢量為 |ψ(t)⟩{displaystyle |psi (t)rangle } 的量子系統，其动力学演化可以用薛定谔方程表示，iℏ∂∂t|ψ(t)⟩=H^|ψ(t)⟩{displaystyle ihbar {frac {partial }{partial t}}|psi (t)rangle ={hat {H}}|psi (t)rangle } ；其中，哈密顿算符 H^{displaystyle {hat {H}}} 对应於量子系统的总能量，ℏ{displaystyle hbar }是約化普朗克常數。根據薛定谔方程，假設時間從t0{displaystyle t_{0}}流易到t{displaystyle t}，則態向量從|ψ(t0)⟩{displaystyle |psi (t_{0})rangle }演化到 |ψ(t)⟩{displaystyle |psi (t)rangle } ，這過程以方程式表示為|ψ(t)⟩=U^(t,t0)|ψ(t0)⟩{displaystyle |psi (t)rangle ={hat {U}}(t,t_{0})|psi (t_{0})rangle } ；其中，U^(t,t0)=e−iH^(t−t0)/ℏ{displaystyle {hat {U}}(t,t_{0})=e^{-i{hat {H}}(t-t_{0})/hbar }} 是時間演化算符。


3. 可觀察量公設：每個可观察量 A{displaystyle A} 都有其對應的厄米算符 A^{displaystyle {hat {A}}} ，而算符A^{displaystyle {hat {A}}}的所有本徵矢量共同組成一個完備基底。


4. 塌縮公設：對於量子系統測量某個可觀察量 A{displaystyle A} ，這動作可以數學表示為將其對應的厄米算符A^{displaystyle {hat {A}}} 作用於量子系統的態矢量 |ψ⟩{displaystyle |psi rangle } ，測量值只能為厄米算符A^{displaystyle {hat {A}}} 的本徵值。在測量後，假設測量值為ai{displaystyle a_{i}}，則量子系統的量子態立刻會塌縮為對應於本徵值ai{displaystyle a_{i}}的本徵態 |ei⟩{displaystyle |e_{i}rangle } 。


5. 
   波恩公設：對於這測量，獲得本徵值 ai{displaystyle a_{i}} 的概率為量子態|ψ⟩{displaystyle |psi rangle }處於本徵態|ei⟩{displaystyle |e_{i}rangle }的概率幅的絕對值平方。^[c]
   

量子態與量子算符

設定斯特恩-革拉赫實驗儀器的磁場方向為z-軸，入射的銀原子束可以被分裂成兩道銀原子束，每一道銀原子束代表一種量子態，上旋|↑⟩{displaystyle |uparrow rangle }或下旋|↓⟩{displaystyle |downarrow rangle }。^[15]:1-4

量子態指的是量子系統的狀態，態向量可以用來抽象地表現量子態。採用狄拉克標記，態向量表示為右矢|ψ⟩{displaystyle |psi rangle }；其中，在符號內部的希臘字母ψ{displaystyle psi }可以是任何符號，字母，數字，或單字。例如，沿著磁場方向測量電子的自旋，得到的結果可以是上旋或是下旋，分別標記為|↑⟩{displaystyle |uparrow rangle }或|↓⟩{displaystyle |downarrow rangle }。^[16]:93-96

對量子態做操作定義，量子態可以從一系列製備程序來辨認，即這程序所製成的量子系統擁有這量子態。^[17]:15-16例如，使用斯特恩-革拉赫實驗儀器，設定磁場朝著z-軸方向，如右圖所示，可以將入射的銀原子束，依照自旋的z-分量分裂成兩道，一道為上旋，量子態為|↑⟩{displaystyle |uparrow rangle }，另一道為下旋，量子態為|↓⟩{displaystyle |downarrow rangle }，這樣，可以製備成量子態為|↑⟩{displaystyle |uparrow rangle }的銀原子束，或量子態為|↓⟩{displaystyle |downarrow rangle }的銀原子束。原本銀原子束的態向量可以按照態疊加原理表示為^[15]:1-4

|ψ⟩=α|↑⟩+β|↓⟩{displaystyle |psi rangle =alpha |uparrow rangle +beta |downarrow rangle }；

其中，α{displaystyle alpha }、β{displaystyle beta }是複值係數，|α|2{displaystyle |alpha |^{2}}、|β|2{displaystyle |beta |^{2}}分別為入射銀原子束處於上旋、下旋的概率，|α|2+|β|2=1{displaystyle |alpha |^{2}+|beta |^{2}=1}。

在斯特恩-革拉赫實驗裏，可以透過測量而得到自旋的z-分量，這種物理量稱為可觀察量，透過做實驗測量可以得到其測值。每一個可觀察量都有一個對應的量子算符；將算符作用於量子態，會使得量子態線性變換成另一個量子態。假若變換前的量子態與變換後的量子態，除了乘法數值以外，兩個量子態相同，則稱此量子態為此算符的本徵態，稱此乘法數值為此算符的本徵值。^[15]:11-12可觀察量的算符也許會有很多本徵值與本徵態。根據統計詮釋，每一次測量所得到的測值只能是其中的一個本徵值，而且，測得這本徵值的機會呈概率性，量子系統的量子態也會改變為對應於本徵值的本徵態。^[16]:106-109例如，自旋的z-分量是個可觀察量Sz{displaystyle S_{z}}，做實驗可以得到的測值為+ℏ/2{displaystyle +hbar /2}或−ℏ/2{displaystyle -hbar /2}。對應於可觀察量Sz{displaystyle S_{z}}的量子算符S^z{displaystyle {hat {S}}_{z}}有兩個本徵值分別為+ℏ/2{displaystyle +hbar /2}、−ℏ/2{displaystyle -hbar /2}的本徵態|↑⟩{displaystyle |uparrow rangle }、|↓⟩{displaystyle |downarrow rangle }，所以將量子算符S^z{displaystyle {hat {S}}_{z}}分別作用於這兩個本徵態，會得到^[15]:11-12

S^z|↑⟩=+ℏ2|↑⟩{displaystyle {hat {S}}_{z}|uparrow rangle =+{tfrac {hbar }{2}}|uparrow rangle }、

S^z|↓⟩=−ℏ2|↓⟩{displaystyle {hat {S}}_{z}|downarrow rangle =-{tfrac {hbar }{2}}|downarrow rangle }。

將量子算符S^z{displaystyle {hat {S}}_{z}}作用於量子態|ψ⟩=α|↑⟩+β|↓⟩{displaystyle |psi rangle =alpha |uparrow rangle +beta |downarrow rangle }，會得到本徵值+ℏ/2{displaystyle +hbar /2}、−ℏ/2{displaystyle -hbar /2}的概率分別為|α|2{displaystyle |alpha |^{2}}、|β|2{displaystyle |beta |^{2}}。假若本徵值為+ℏ/2{displaystyle +hbar /2}，則量子態|ψ⟩{displaystyle |psi rangle }會塌縮為量子態|↑⟩{displaystyle |uparrow rangle }；假若本徵值為−ℏ/2{displaystyle -hbar /2}，則量子態|ψ⟩{displaystyle |psi rangle }會塌縮為量子態|↓⟩{displaystyle |downarrow rangle }。

动力学演化

在量子力學公設裏，第二項直接提到量子系統的動力學演化，其遵守含時薛丁格方程式，因此，量子態的演化在任意時刻可以被完全預測，具有連續性、命定性與可逆性。第四項提到，當對於量子系統作測量時，其量子態會塌縮至幾個本徵態中的一個本徵態，具有不連續性、概率性與不可逆性。怎樣調和這兩種不同的行為，一種是關於量子態的自然演化，另一種是關於測量引發的演化，這仍舊是未解決的物理學問題。^[17]:7-11

量子系統的动力学演化可以用不同的绘景来表現。通过重新定义，这些不同的繪景可以互相變换，它们实际上是等價的。假若要專注分析量子態怎樣隨著時間的流易而演化，時間演化算符怎樣影響量子態，則可採用薛丁格繪景。假若要專注了解對應於可觀察量的算符怎樣隨著時間的流易而演化、時間演化算符怎樣影響這些算符，則可採用海森堡绘景。^[15]:80-89

主要論題

测量过程

量子力学与經典力学的一个主要区别，在於怎樣理論論述测量过程。在經典力学裏，一个物理系统的位置和动量，可以同时被无限精确地确定和预測。在理论上，测量過程对物理系统本身，并不會造成任何影响，并可以无限精确地进行。在量子力学中则不然，测量过程本身会对系统造成影响。^[18]

怎樣才能正確地理論描述對於一个可观察量的测量？設定一个量子系统的量子态，首先，將量子態分解为该可观察量的一组本征态的线性组合。测量过程可以視為對於本征态的一个投影，测量结果是被投影的本征态的本征值。假設，按照某種程序製備出一個系綜，在這系綜裏，每一個量子態都與這量子態相同，現在對於這系綜裏的每一個量子態都進行一次測量，則可以获得所有可能的测量值（本徵值）的机率分布，每个测量值的概率等於量子態處於對應的本征态的概率幅的绝对值平方。^{[16]:36-37, 96-100}

因此，假設對於两个不同的可觀察量 A{displaystyle A} 和 B{displaystyle B}做测量，改變測量顺序，例如從AB{displaystyle AB}改變為BA{displaystyle BA}，則可能直接影响测量结果。假若測量結果有所不同，則稱這兩個可觀察量為不相容可觀察量；否則，稱這兩個可觀察量為相容可觀察量。以數學術語表達，兩個不相容可觀察量A{displaystyle A} 和 B{displaystyle B}的對易算符不等於零：^[16]:110-112

[A^,B^] =def A^B^−B^A^≠0{displaystyle [{hat {A}},{hat {B}}] {stackrel {def}{=}} {hat {A}}{hat {B}}-{hat {B}}{hat {A}}neq 0}。

不确定性原理

不确定性原理表明，越能準確地設定粒子的位置，則越不能準確地設定粒子的動量，反之亦然，^[19]:引言以方程式表示為^[16]:110-114

ΔxΔp≥ℏ2{displaystyle Delta xDelta pgeq {frac {hbar }{2}}}；

其中，Δx{displaystyle Delta x}、Δp{displaystyle Delta p}分別為位置、動量的不確定性。

設想一個定域性的波包，假設波包的尺寸為L{displaystyle L} ．從計數波包的週期數N{displaystyle N}，可以知道其波數k{displaystyle k}：

k=2πN/L{displaystyle k=2pi N/L}。

假若，計數N{displaystyle N}的不確定性為ΔN=1{displaystyle Delta N=1}，那麼，波數的不確定性是

Δk=2π/L{displaystyle Delta k=2pi /L}。

根據德布羅意假說，P=ℏk{displaystyle P=hbar k}。因此，動量的不確定性是

ΔP=ℏΔk=hL{displaystyle Delta P=hbar Delta k={frac {h}{L}}}。

由於粒子位置的不確定性是ΔX≈L/2{displaystyle Delta Xapprox L/2}，所以，這兩個不相容可觀察量的不確定性為^[20]:5-6

ΔPΔX≈h/2{displaystyle Delta PDelta Xapprox h/2}。

全同粒子

在無限深方形阱裏，兩個全同費米子的反對稱性波函數繪圖。^[d]

在無限深方形阱裏，兩個全同玻色子的對稱波函數繪圖。^[e]

粒子具有很多種物理性質，例如質量、電荷、自旋等等。假若兩個粒子具有不同的性質，則可以藉著測量這些不同的性質來區分這兩個粒子。根據許多實驗獲得的結果，同種類的粒子具有完全相同的性質，例如，宇宙裏所有的電子都帶有相等數量的電荷。因此，無法依靠物理性質來區分同種類的粒子，必需使用另一種區分法，即跟蹤每一個粒子的軌道。只要能夠無限精確地測量出每一個粒子的位置，就不會搞不清楚哪一個粒子在哪裡。這個適用於經典力學的方法有一個問題，那就是它與量子力學的基本原理相矛盾。根據量子理論，在位置測量期間，粒子並不會保持明確的位置。粒子的位置具有概率性。隨著時間的流易，幾個粒子的量子態可能會移動蔓延，因此某些部分會互相重疊在一起。假若發生重疊事件，给每个粒子“挂上一个标签”的方法立刻就失去了意义，就無法區分在重疊區域的兩個粒子。^[16]:201ff

全同粒子所呈現出的不可区分性，对量子态的对称性，以及多粒子系统的统计力学，有深远的影响。比如说，一个由全同粒子组成的多粒子系统量子态，在交换两个粒子“1”和粒子“2”时，可以证明，不是对称的 (|ψ12⟩=+|ψ21⟩){displaystyle (|psi _{12}rangle =+|psi _{21}rangle )} ，就是反对称的 (|ψ12⟩=−|ψ21⟩){displaystyle (|psi _{12}rangle =-|psi _{21}rangle )} 。具有对称性的粒子被称为玻色子，具有反对称性的粒子被称为费米子。此外自旋的对换也形成对称：自旋为半数的粒子（如电子、质子和中子）是反对称的，因此是费米子；自旋为整数的粒子（如光子）是对称的，因此是玻色子。

由於费米子系統具有反对称性，費米子遵守泡利不相容原理，即两个费米子无法占据同一状态^[15]:451。这个原理拥有极大的实用意义。它表明，在由原子组成的物质世界裡，电子无法同时占据同一状态，因此在最低状态被占据後，下一个电子必须占据次低的状态，直到所有的状态均被满足为止。这个现象决定了物质的物理和化学特性^{[16]:204,214,218-221}。

费米子与玻色子的状态的热分布也相差很大：玻色子遵循玻色-爱因斯坦统计，而费米子则遵循费米-狄拉克统计^[15]:450。

量子纠缠

假設一個零自旋中性π介子衰變成一個電子與一個正電子，這兩個衰變產物各自朝著相反方向移動，雖然彼此之間相隔一段距離，它們仍舊會發生量子糾纏現象。

假設兩個粒子在經過短暫時間彼此耦合之後，單獨攪擾其中任意一個粒子，儘管兩個粒子之間可能相隔很長一段距離，還是會不可避免地影響到另外一個粒子的性質，這種關聯現象稱為量子糾纏。往往由多个粒子组成的量子系统，其状态无法被分离为其组成的单个粒子的状态，在这种情况下，单个粒子的状态被称为是纠缠的。纠缠的粒子有惊人的特性，这些特性违背一般的直觉。比如说，对一个粒子的测量，可以导致整个系统的波包立刻塌缩，因此也影响到另一个、遥远的、与被测量的粒子纠缠的粒子。这个现象并不违背狭义相对论，因为在量子力学的层面上，在测量粒子前，它们不能被單獨各自定义，实际上它们仍是一个整体。不过在测量它们之后，它们就会脱离量子纠缠的状态。^{[17]:27-31:120ff}

量子退相干

作为一个基本理论，量子力学原则上，应该适用于任何大小的物理系统，也就是说不仅限于微观系统，那么，它应该提供一个过渡到宏观經典物理的方法。量子现象的存在提出了一个问题，即怎样从量子力学的观点，解释宏观系统的經典现象。尤其无法直接看出的是，量子力学中的量子疊加，在宏观世界怎樣呈現出來。1954年，爱因斯坦在给马克斯·玻恩的信中，就提出了怎样从量子力学的角度，来解释宏观世界的物理現象的问题，他指出仅仅量子力学现象太“小”无法解释这个问题。^[21]:62-63这个问题的另一个例子是由薛定谔提出的薛定谔猫的思想实验。^[21]:2

後來，物理學者领会到，上述的思想实验，实际而言并不合乎現實，因为它们忽略了不可避免地与周围环境的相互作用，量子系統會因為這相互作用與環境關聯在一起。處於疊加態的量子系統非常容易受周围环境的影响，而且隨著時間流易，這量子系統會與環境永無休止地越加深入糾纏，這現象稱為「馮紐曼無窮鏈」（Von Neumann's infinite chain）。在疊加態裏，幾個相互正交的量子態疊加在一起，彼此相干。量子退相干是一種過程，能夠將量子系統的約化密度矩陣對角化，而相干性質就是表示於這約化密度矩陣的非對角元素，所以，疊加態的相干性質會快速消失，無法再被探測到，從而呈現出經典的統計性質。雖然量子系統的疊加態不再具有相干性質，整個量子系統與環境共同組成的聯合態仍舊具有相干性質。^{[17]:19-21, 136-138[22]}

对于量子计算机来说，量子退相干也有实际意义。在一台量子计算机中，需要多个量子状态尽可能地长时间保持叠加。退相干时间短是一个非常大的技术问题，因為它會削弱量子疊加效應，但它也是一個必需的因素，因為儲存在計算機內的數據必需經過量子測量被讀出來。^[23]

与其它物理理论的关系

經典物理

波動光學在短波長極限成為幾何光學，類似地，量子力學在普朗克常數趨零極限成為經典力學。基本而言，在普朗克常數趨零極限，可以從量子力學的薛丁格方程式推導出經典力學的哈密頓-亞可比方程式。詳盡細節，請參閱條目哈密頓-亞可比方程式。^[24]

量子力學的預測已被實驗核對至極高準確度，是在科學領域中，最為準確的理論之一。^[7]對應原理實現經典力學與量子力學之間的對應關係，根據對應原理，假若量子系统已達到某「經典極限」，則其物理行為可以很精确地用經典理论來描述；這經典極限可以是大量子數極限，也可以是普朗克常數趨零極限。實際而言，许多宏观系统都是用經典理论（如經典力学和电磁学）来做精确描述。因此在非常“大”的系统中，量子力学的特性應該会逐漸與經典物理的特性相近似，两者必須相互符合。^[25]:190-191

对应原理對於建立一个有效的量子力学模型是很重要的辅助工具。量子力学的数学基础相當廣泛寬鬆，它僅只要求量子系統的態向量屬於希尔伯特空间，其可观察量是线性的厄米算符，它并没有规定在实际情况下，应该选择哪一种希尔伯特空间、哪些厄米算符。因此，在实际情况下，必须选择相应的希尔伯特空间和算符来描写一个特定的量子系统。而对应原理则是做出这个选择的一个重要辅助工具。这个原理要求量子力学所做出的预言，在越来越大的系统中，逐渐近似經典理论的预言。这个大系统的极限，被称为“經典极限”或者“对应极限”。因此可以使用启发法的手段，来建立一个量子力学的模型，而这个模型的极限，就是相应的經典物理学的模型。^{[25]:190-191[26]:3ff}

在經典系統與量子系統之間，量子相干是一種很明顯可以用來區分的性質，具有量子相干性的電子、光子等等微觀粒子可以處於量子疊加態，不具有量子相干性的棒球、老虎等等宏觀系統不可以處於量子疊加態。量子退相干可以用來解釋這些行為。一種應用這性質來區分的工具是貝爾不等式，遭到量子糾纏的系統不遵守貝爾不等式，而量子退相干能夠將量子糾纏性質變換為經典統計性質，系統的物理行為因此可以用隱變數理論解釋，不再不遵守貝爾不等式。^[27]:80-82簡略而言，量子干涉是將幾個量子態的量子幅總和在一起，而經典干涉則是將幾個經典波動的波強總和在一起。對於微觀物體，整個系統的延伸尺寸超小於相干長度，因此會產生長程量子糾纏與其它非定域現象，一些量子系統的特徵行為。通常，量子相干不會出現於宏觀系統。^[28]

狹義相对论

原本量子力學的表述所針對的模型，其對應極限為非相對論性古典力學。例如，眾所皆知的量子諧振子模型使用了非相對論性表達式來表達其動能，因此，這模型是古典諧振子的量子版本。^[16]:40-59

早期，對於合併量子力学与狭义相对论的试图，涉及到使用協變方程式，例如，克莱因-戈尔登方程或狄拉克方程式，来取代薛定谔方程。这些方程雖然能夠很成功地描述许多量子现象，但它们目有某些不滿意的問題，它们无法描述在相对论性状況下，粒子的生成和湮滅。完整的相对论性量子理论需要量子场论的關鍵发展。量子场论能夠将场量子化（而不是一組固定數量的粒子）。第一个量子场论是量子电动力学，它可以精確地描写电磁相互作用。^[15]:486-514量子電動力學其對於某些原子性質的理論預測，已被證實準確至10⁸分之一。^[29]:7

對於描述电磁系统，時常不需要使用到量子场论的全部功能。比较简单的方法，是将带电粒子当作处於經典电磁场中的量子力学物体。这个手段从量子力学的初期，就已经被使用了。比如说，氢原子的电子状态，可以近似地使用經典的 1/r{displaystyle 1/r} 庫侖勢来计算。这就是所谓的半經典方法。但是，在电磁场中的量子起伏起一个重要作用的情况下（比如带电粒子发射一颗光子）这个近似方法就失效了。^[16]:145-160

粒子物理學

專門描述强相互作用、弱相互作用的量子場論已發展成功。强相互作用的量子场论稱為量子色动力学，这个理论描述亞原子粒子，例如夸克、胶子，它們彼此之间的相互作用。弱相互作用与电磁相互作用也被統一為單獨量子場論，稱為电弱相互作用。^{[4]:1234-1236}

廣義相對論

量子引力是對引力場進行量子化描述的理論，屬於萬有理論之一。物理學者發覺，建造引力的量子模型是一件非常艱難的研究。半經典近似是一種可行方法，推導出一些很有意思的預測，例如，霍金輻射等等。可是，由於廣義相對論（至今為止，最成功的引力理論）與量子力學的一些基礎假說相互矛盾，表述出一個完整的量子引力理論遭到了嚴峻阻礙。嘗試結合廣義相對論與量子力學是熱門研究方向，為當前的物理學尚未解决的問題。當前主流嘗試理論有：超弦理論、迴圈量子重力理論等等。^[30][31]

哲学观点

未解決的物理學問題：量子理論的描述怎樣成為做實驗所觀查到的大自然實在，這包括量子態疊加、波函數塌縮、量子去相干等等？換句話說，這是一種測量問題，造成波函數塌縮為確定態的量子測量所倚賴的機制為何？

量子力学是經歷最严格验证的物理理论之一。至今为止，尚未找到任何能夠推翻量子力学的实验数据。大多数物理学者认为，“几乎”在所有情况下，它正确地描写能量和物质的物理性质。虽然如此，量子力学中，依然存在着概念上的弱点和缺陷，除前面所述關於万有引力的量子理论的缺乏以外，現今，对於量子力学的詮释依然存在着嚴重争议。^[32][27]:4-5

從初始到現今，量子力學的各種反直覺論述與結果一直不停地引起在哲學、詮釋方面的強烈辯論。甚至一些基礎論點，例如，馬克斯·玻恩關於概率幅與概率分佈的基本定則，也需要經過數十年的嚴格思考論證，才被學術界接受。^[f]理察·費曼曾經說過一句銘言：「我認為我可以有把握地說，沒有人懂得量子力學！」^[33]史蒂文·溫伯格承認：「依照我現在的看法，完全令人滿意的量子力學詮釋並不存在。」^[34]

雖然在發表後已經過七十幾年光陰，哥本哈根詮釋仍舊是最為物理學者接受的對於量子力學的一種詮釋。它的主要貢獻者是尼尔斯·玻尔與沃纳·海森堡。根據這種詮釋，量子力學的概率性論述不是一種暫時補丁，並且最終將會被一種命定性理論取代，它必須被視為一種最終拋棄經典因果論思維的動作。在這裡，任何量子力學形式論的良好定義的應用必須將實驗設置納入考量，這是因為不同實驗狀況獲得的結果所具有的互補性。^[17]:15-16

身為量子理論的創始者之一的愛因斯坦很不滿意這種非命定性的論述。他認為量子力學不具有完備性，他提出一系列反駁論述，其中最著名的就是愛因斯坦-波多爾斯基-羅森佯謬。這佯謬建立於定域實在論。假設局區域實在論成立，則量子力學不具有完備性。接近三十年以後，約翰·貝爾發佈論文表示，對於這個佯謬稍加理論延伸，就會導致對於量子力學與定域實在論出現不同的預言，因此可以做實驗檢試量子世界到底與哪種預言一致。^[35][36]為此，完成了很多相關實驗，這些實驗確定量子力學的預言正確無誤，定域實在論無法描述量子世界。^[37]

休·艾弗雷特三世提出的多世界诠释认为，量子理论所做出的可能性的预言，全部會同步实现，这些现实成为彼此之间毫無關聯的平行宇宙。在这種诠释裏，波函数不塌缩，它的发展是决定性的。但是由於隻身观察者无法存在於所有的平行宇宙裏，只能观察在身處的宇宙內發生的事件，而無法觀察到其它平行宇宙內發生的事件。这種诠释不需要特殊處理测量動作。在这理论裏，薛定谔方程無論何處無論何時都成立。對於任何測量動作，必須將整個系統，測量儀器與被測量物體，全部納入薛定谔方程的運算。^[38][39]測量儀器與被測量物體所有可能的量子態都存在於一種真實的量子疊加，形成了糾纏態。雖然平行宇宙具有命定性，觀察者意識到由概率主導的非命定行為，因為觀察者只能觀察到自身所在的宇宙。多世界诠释能夠透過貝爾的檢試實驗。近期研究發展將多世界诠释與量子退相干理論合併在一起來解釋主觀的波函數塌縮。由於量子退相干機制，糾纏態會快速地演化為經典混合態。^[40]

戴维·玻姆提出了一種非定域性的隱變量理論，稱為導航波理論。在这種詮释裏，波函数被理解为粒子的一个導航波。从结果上，这个理论预言的实验结果，与非相对论哥本哈根诠释的预言完全一样，因此，使用实验手段无法鉴别这两个解释。虽然这个理论的预言是命定性的，但是由於不确定原理无法推测出隐变量的精确状态，其结果跟哥本哈根诠释的結果一样，使用導航波理論来解释，实验的结果具有概率性。至今为止，还不能确定这个解释是否能够扩展到相对论量子力学上去。路易·德布罗意和其他人也提出过类似的隐变量解释。^[41][42]

应用

在许多现代技术装备中，量子效应起了重要的作用，例如，激光的工作機制是愛因斯坦提出的受激發射、电子显微镜利用電子的波粒二象性來增加解析度、原子钟使用束縛於原子的電子從一個能級躍遷至另一個能級時所發射出的微波信號的頻率來計算與維持時間的準確性、核磁共振成像倚賴核磁共振機制來探測物體內部的結構。对半导体的研究导致了二极管和三极管的发明，這些都是現代電子系統與電子器件不可或缺的元件。^[27]:5-10

以下列出了一些量子力學的應用，但實際上其應用並不限於這些領域。

电子器件

量子力学在电子器件中得到了广泛应用。比如发光二极管在日常照明中应用中越来越广泛^[43]。现代计算机的基础，微处理器，由上亿个半导体晶体管集成，且随着晶体管数量的增加，晶体管中的量子效应越来越明显。量子力学对于解释和模拟半导体器件中的电学、光学、热学性质等尤其重要。^[1]:382-386

量子力学还是量子隧穿器件工作的基础。比如USB非易失性闪存中，信息的存储和读取都通过量子隧穿实现。^[44]

超导电子器件也与量子力学有着密切的关系^[45]。

计算机

相比于晶体管等电子器件，量子计算机的研制则更为前沿。在一些特定算法下，量子计算机的速度会比经典架构的计算机快成千上万倍（比如量子退火算法）。经典计算机使用0和1作为比特，而量子计算机则使用量子位作为基本单位。量子位由不同的电子态叠加形成。^[27]:91-100

宇宙學

由FIRAS儀器對COBE觀測的宇宙微波背景輻射光譜，為最精確測量的黑體輻射光譜性質，^[46]即使將圖像放大，誤差範圍也極小，無法由理論曲線中分辨觀測數據。

量子力學能夠用來解釋很多奇異的宇宙現象，例如，宇宙微波背景的頻譜可以用普朗克黑體輻射定律來解釋。宇宙微波背景證實了大爆炸理論的正確無誤，自此，穩態理論開始式微。從宇宙微波背景可以推論，早期宇宙非常炙熱、對於電磁輻射不透明、具有均質性與各向同性，是標準的黑體。^{[47]:273[48]:152}

在恆星的生命終點，當所有核燃料都已用盡，恆星會開始引力坍缩的過程，最終可能變為白矮星、中子星或黑洞。這是因為包立不相容原理的作用。由於電子遵守包立不相容原理，因此在坍缩時，假若電子簡併壓力能夠克服引力，就會形成白矮星，否則會繼續坍缩，由於中子也遵守包立不相容原理，這時假若中子簡併壓力能夠克服引力，則會形成中子星，否則就會坍缩成黑洞。^[49]:286-287

化学

任何物质的化学性質，均是由其原子或分子的电子结构所决定的。通过解析包括了所有相关的原子核和电子的多粒子薛定谔方程，可以计算出该原子或分子的电子结构。在实践中，人们认识到，要计算这样的方程实在太复杂，對於許多案例，必需使用简化的模型，找到可行的數學計算方法，才能夠找到近似的电子结构，從而确定物质的化学性質。^[50]:193-195實際上，量子電動力學是化學的基礎原理^[51]。

量子力學可以詳細描述原子的電子結構與化學性質。對於只擁有一個束縛電子的氫原子，薛丁格方程式有解析解，可以計算出相關的能級與氫原子軌域，而且能級符合氫原子光譜實驗的數據，從每一種氫原子軌域可以得到對應的電子概率分佈。對於其它種原子（多電子原子），薛丁格方程式沒有解析解，只能得到近似解，可以計算出近似氫原子軌域的哈特里原子軌域，形狀相同，但尺寸與能級模式不一樣。使用哈特里原子軌域，可以解釋原子的電子結構與化學性質，週期表的元素排列。^[50]:193-195

量子力學能夠解釋，在分子裏的束縛電子怎樣將分子內部的原子綑綁在一起。對於最為簡單，只擁有一個束縛電子的氫分子離子H₂⁺，應用玻恩–奥本海默近似（兩個原子核固定不動），薛丁格方程式有解析解，可以計算出它的分子軌域。但是對於其它更為複雜的分子，薛丁格方程式沒有解析解，只能得到近似解，只能計算出近似的分子軌域。理论化学中的分支，量子化学和计算化学，專注於使用近似的薛定谔方程，来计算复杂的分子的结构及其化学性質。^[50]:235ff

信息学

目前的研究聚焦於找到可靠與能夠直接处理量子态的方法。量子系統擁有一種特性，即對於量子數據的測量會不可避免地改變數據，這種特性可以用來偵測出任何竊聽動作。倚賴這特性，量子密碼學能夠保證通信安全性，使得通信双方能够产生并分享一个随机的，安全的密钥，来加密和解密信息。比較遙遠的目標是發展出量子電腦。由於量子态具有量子叠加的特性，理论而言，量子電腦可以達成高度并行计算，其計算速度有可能以指數函數快過普通電腦。另外，應用量子纏結特性與經典通訊理論，量子遙傳能夠將物體的量子態從某個位置傳送至另一個位置。這是正在積極進行的一門學術領域。^[52]

註釋

参考文献

外部链接

• 
  国立交通大学物理系視聽教學：量子力学导论。

参见

• 普朗克單位制