Rearuh

可見光譜只佔有寬廣的電磁波譜的一小部分。

電磁辐射，又稱電磁波，是指同相振盪，且互相垂直的電場與磁場，在空間中以波的形式傳遞能量和動量，其傳播方向垂直於電場與磁場的振盪方向。

電磁輻射的載體為光子，不需要依靠介質傳播，在真空中的傳播速度为光速。電磁輻射可按照頻率分類，從低頻率到高頻率，主要包括無線電波、微波、紅外線、可見光、紫外線、X射線和伽馬射線。人眼可接收到的電磁輻射，波長大約在380至780nm之間，稱為可見光。只要是本身溫度大於絕對零度的物體，除了暗物質以外，都可以發射電磁輻射，而世界上並不存在温度等於或低於絕對零度的物體，因此，人們周邊所有的物體時刻都在進行電磁輻射。儘管如此，只有處於可見光频域以内的電磁波，才可以被人們肉眼看到，對於不同的生物，各種電磁波頻段的感知能力也有所不同。

發現歷史

詹姆斯·馬克士威

在可見光波長以外的電磁輻射被發現於19世紀初期。紅外線輻射的發現歸因於天文學家威廉·赫歇爾，他於1800年在倫敦皇家學會發表了他的成果。^[1]

電磁波首先由詹姆斯·馬克士威於1865年預測出來，而後由德国物理学家海因里希·赫兹於1887年至1888年間在实验中证实存在。^[2][3]馬克士威推導出電磁波方程式，一種波動方程式，這清楚地顯示出電場和磁場的波動本質。因為電磁波方程式預測的電磁波速度與光速的測量值相等，馬克士威推論光波也是電磁波^[4][5]:283。無線電波被海因里希·赫兹在1887年第一個刻意產生，使用電路計算出比可見光低得多的頻率上產生振盪，随之產生了由麥克斯韋方程所建議的振盪電荷和電流。赫茲還開發檢測這些電波的方法，並產生和特徵化这些後來被稱為無線電波和微波。^[6]:286,7

威廉·倫琴發現並命名了X射線。 在1895年11月8日的應用於真空管上的高電壓試驗後，他注意到在附近的鍍膜玻璃板的熒光。在一個月內，他發現了X射線的主要性質。^[6]:307

概念

三種不同的電磁波波模 (mode)（藍、綠、紅），x-軸長度尺度是微米。

電動力學專門研究電磁波的物理行為，是電磁學的分支。在電動力學裏，根據馬克士威方程組，隨著時間變化的電場產生了磁場，反之亦然。因此，一個振盪中的電場會產生振盪的磁場，而一個振盪中的磁場又會產生振盪的電場，這樣子，這些連續不斷同相振盪的電場和磁場共同地形成了電磁波^{[7]:326[8]:894-897}。

電場，磁場都遵守疊加原理。^[9]:9因為電場和磁場都是向量場，所有的電場向量和磁場向量都適合做向量加運算。例如，一個行進電磁波，入射於一個介質，會引起介質內的電子振盪，因而使得它們自己也發射電磁波，因而造成折射或繞射等等現象^[8]:959-968。

在非線性介質內（例如，某些晶體），電磁波會與電場或磁場產生交互作用，這包括法拉第效應^[10]:366-368、克爾效應等等^[11]。

當電磁波從一種介質入射於另一種介質時，假若兩種介質的折射率不相等，則會產生折射現象，電磁波的方向和速度會改變。斯涅爾定律專門描述折射的物理行為^[7]:388。

光通過三棱镜后，因色散造成不同顏色折射至不同的角度，讓白光形成可见光谱。

假設，由很多不同頻率的電磁波組成的光波，從空氣入射於稜鏡。而因為菱鏡內的材料的折射率跟電磁波的頻率有關，會產生色散現象：光波會色散成一組可觀察到的電磁波譜^[7]:398-405。

量子電動力學是描述電磁輻射與物質之間的相互作用的量子理論^[12]。電磁波不但會展示出波動性質，它還會展示出粒子性質（參閱波粒二象性）。這些性質已經在很多物理實驗中證實，例如，楊氏雙縫實驗展示出電磁波的波動性質^[8]:964-967、光電效應展示出電磁波的粒子性質^{[8]:1060-1062}。有時候，波動性質和粒子性質會出現於同一個實驗，例如，在雙縫實驗裏，當單獨光子被發射於兩條細縫時，單獨光子會穿過這兩條細縫，自己與自己干涉，就好像波動運動一樣。可是，它只會被光電倍增管偵測到一次^{[8]:1066-1067}。當單獨光子被發射於馬赫-曾德爾干涉儀或其它種干涉儀時，也會觀測到類似的自我干涉現象^[13]:37-38。

波動模型

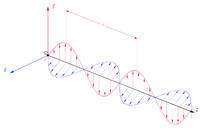
電磁波是橫波，電場方向與磁場方向相互垂直，又都垂直於傳播方向。

波是由很多前後相繼的波峰和波谷所組成，兩個相鄰的波峰或波谷之間的距離稱為波長。電磁波的波長有很多不同的尺寸，從非常長的無線電波（有一個足球場那麼長）到非常短的伽馬射線（比原子半徑還短）^[8]:890。

描述光波的一個很重要的物理參數是頻率。一個波的頻率是它的振盪率，國際單位制單位是赫茲。每秒鐘振盪一次的頻率是一赫茲。頻率與波長成反比：

v=νλ{displaystyle v=nu lambda ,!}；

其中，v{displaystyle v,!}是波速（在真空裏是光速；在其它介質裏，小於光速），ν{displaystyle nu ,!}是頻率，λ{displaystyle lambda ,!}是波長。

當波從一個介質傳播至另一個介質時，波速會改變，但是頻率不變^[8]:961。

干涉是兩個或兩個以上的波，疊加形成新的波樣式。假若這幾個電磁波的電場同方向，磁場也同方向，則這干涉是建設性干涉；反之，則是摧毀性干涉^[8]:959-962。

電磁波的能量，又稱為輻射能。這能量，一半儲存於電場，另一半儲存於磁場。用方程式表達^[8]:897-899：

u=12μ0B2+ϵ02E2{displaystyle u={frac {1}{2mu _{0}}}B^{2}+{frac {epsilon _{0}}{2}}E^{2},!}；

其中，u{displaystyle u,!}是單位體積的能量，E{displaystyle E,!}是電場數值大小，B{displaystyle B,!}是磁場數值大小，ϵ0{displaystyle epsilon _{0},!}是電常數，μ0{displaystyle mu _{0},!}是磁常數。

粒子模型和量子理論

電磁輻射擁有像粒子的性質。電磁輻射是由離散能量的波包形成的，這波包又稱為量子，或光子。光子的能量與電磁輻射的頻率成正比。由於光子可以被帶電粒子吸收或發射，光子承擔了一個重要的角色：能量的傳輸者。根據普朗克-愛因斯坦關係式，光子的能量是^{[14]:17, 24}

E=hν{displaystyle E=hnu ,!}；

其中，E{displaystyle E,!}是能量，h{displaystyle h,!}是普朗克常數，ν{displaystyle nu ,!}是頻率。

光子的動量p{displaystyle p,!}與頻率、波長之間的關係為^[8]:1063

p=Ec=hνc=hλ{displaystyle p={frac {E}{c}}={frac {hnu }{c}}={frac {h}{lambda }},!}；

當一個光子被原子吸收的同時，也會激發它的束縛電子，將電子的能級升高。假若光子給出的能量足夠大，電子可能會逃離原子核的束縛吸引，成為自由電子。這程序稱為光離化（英语：photoionization）^[15] 。逆反過來，一個躍遷至較低能級的電子，會發射一個能量等於能級差額的光子。由於原子內的電子能級是離散的，每一種原子只能發射和吸收它的特徵頻率的光子^[16]。

綜合在一起，這些效應解釋了光波的吸收光譜。在介質內的原子，因為吸收不同頻率的光波，造成了光譜的"暗線"。光波所通過的介質的組成成分，決定了吸收光譜的表徵。舉例而言，一個遙遠的恆星的光譜，其暗線與恆星的大氣塵的原子組合有關．這些暗線對應於原子的容許能級。類似的現象也會發生於光波的發射．當電子從高能級量子態躍遷至低能級量子態的同時，光波也會被發射出來，其能量等於兩個能級的差值。這現象顯現於星雲的發射光譜。今天，科學家用這現象來觀測恆星的內部結構．這現象的紅移被用來計算恆星離地球的距離。

傳播速度

呈加速運動的電荷或隨著時間而變化的電磁場，會產生電磁輻射。在自由空間裏，電磁輻射以光速傳播。準確的計算其物理行為必須引用推遲時間的概念。這會增加電場和磁場的表達式的複雜程度（參閱傑斐緬柯方程式）。這些多加的項目詳細地描述電磁輻射的物理行為。當任意一根導線（或別種導電體，像天線）傳導交流電的時候，同頻率的電磁輻射也會被發射出來^[7]。

在量子層次面，當帶電粒子的波包振盪或加速時，會產生電磁輻射帶電粒子的量子態可以用幾個本徵量子態的含時形式的疊加來表達（請參閱雙態系統）。當系統處於穩定狀態時，由於含時形式會被其複共軛刪除，帶電粒子處於每一個本徵量子態的機率是常數。但是，當系統被微擾時（例如，外電場被開啟），機率變為跟時間有關。帶電粒子處於某本徵量子態的機率會隨時間而變化。這樣，帶電粒子會從某個本徵量子態躍遷至另外一個本徵量子態，因而產生電磁輻射^[16]。

依狀況的不同，電磁輻射的物理行為，可能像波動，又可能像粒子。從波動角度，電磁輻射的主要物理特徵是速度、波長、頻率。從粒子角度，電磁輻射是由一群稱為光子的粒子組成。每一個光子的能量E{displaystyle E,!}與波動的頻率ν{displaystyle nu ,!}的關係則是由普朗克關係式給出：

E=hν{displaystyle E=hnu ,!}；

其中，h{displaystyle h,!}是普朗克常數。

不論是粒子還是波動，電磁輻射必然遵守一條定則：不管觀察者的速度有多快或多慢，相對於觀察者，電磁波永遠以光速傳播於真空。愛因斯坦從這洞察發展出狹義相對論，成為狹義相對論的第二條基本原理。

在其它不同於真空的介質內，電磁波傳播的速度會小於光速。一個介質的折射率n{displaystyle n,!}是光速c{displaystyle c,!}與電磁波傳播於介質的速度v{displaystyle v,!}的比例：

n=c/v{displaystyle n=c/v,!}。

熱輻射

物質的基本結構，是由一群帶電粒子，以各種不同的方式結合組成。當電磁波入射於物質時，會造成物質的帶電粒子的振盪和能量增加。這些能量最終的命運依狀況而定。它們很可能會立刻被重新輻射，成為反射輻射或透射輻射。它們也很可能會消散成為物質內的其它微觀運動，達成熱平衡後，再轉以熱能的形式出現。除了少數像荧光、非線性光學效應（nonlinear optical effect）、光化學反應（photochemical reaction） 和光生伏打效應（photovoltaic effect）等等例子以外，被吸收的電磁波大多會直接地存入其能量，因而將物質加熱。對於紅外輻射和非紅外輻射，都會發生這樣的物理行為。強烈的無線電波能夠熱灼傷活生生的細胞組織，也能夠煮熟食物。紅外線雷射，足夠強烈的可見光雷射和紫外線雷射，都可以很容易地點燃紙張。離子化電磁波可以使得物質內的電子擁有高動能，因而破壞其化學鍵。但是在電子與其它原子碰撞多次後，最終大部分的能量會轉換為熱能。這整個程序只需短短的幾分之一秒。很多人士都認為，紅外線波是熱的一種形式，而其它電磁波不是．這是一個錯誤的物理概念。任何被吸收的電磁波都可以使物質加熱。

吸收輻射的逆反程序是熱輻射。在物質內部大部分的熱能都歸功於帶電粒子的隨機運動。這能量可以從物質內被輻射出。形成的輻射可能後來又被另外一個物質吸收。存入的能量會使物質加熱。熱輻射是熱傳輸的一個很重要的機制。

在一個不透明的空腔內，在熱平衡狀況，電磁波可以等效地視為熱能的一種形式，擁有最大的輻射熵。就像物質一樣，電磁波的熱力勢也是良好定義的。空腔內的熱輻射的能量密度（參閱普朗克定律）是

UV=8π5(kT)415(hc)3{displaystyle {U over V}={frac {8pi ^{5}(kT)^{4}}{15(hc)^{3}}},!}；

其中，U{displaystyle U,!}是空腔中電磁場的總能量，V{displaystyle V,!}是空腔的體積，k{displaystyle k,!}是波茲曼常數，T{displaystyle T,!}是空腔內部溫度，c{displaystyle c,!}是光速。

取對於溫度的導數，電磁場的有效比熱容量CV{displaystyle C_{V},!}是

CV=32π5k4T315(hc)3{displaystyle C_{V}={frac {32pi ^{5}k^{4}T^{3}}{15(hc)^{3}}},!}。

電磁波譜

按照波長長短，從長波開始，電磁波可以分類為無線電波、微波、紅外線、可見光、紫外線、X-射線和伽馬射線等等。普通實驗使用的光譜儀就足以分析從2  奈米到2500 奈米波長的電磁波。使用這種儀器，可以得知物體、氣體或甚至恆星的詳細物理性質。這是天文物理學的必備儀器。例如，因為超精細分裂，氫原子會發射波長為21.12公分的無線電波^[17]。

人類眼睛可以觀測到波長大約在400 奈米和700  奈米之間的電磁輻射，稱為『可見光』。

每一種電極性分子，會對應著某些特定頻率的微波，使得電極性分子隨著振蕩電場一起旋轉，這機制稱為電介質加熱（dielectric heating）。由於這種機制（不是熱傳導機制），電極性分子會吸收微波的能量。微波爐就是應用這運作原理，通過水分子的旋轉，更均勻地將食物加熱，減少等候時間。

从电磁理论推导

馬克士威方程組可以描述電磁波的普遍物理现象。在自由空間裏，源項目等於零（源電荷等於零，源電流等於零）。除了沒有任何事發生的解以外（電場和磁場都等於零），方程式仍舊允許不簡單的解，電場和磁場隨著時間和位置變化^[7]。採用國際單位制，處於自由空間狀況的馬克士威方程組表達為

∇⋅E=0{displaystyle nabla cdot mathbf {E} =0,!}、（1）

∇×E=−∂B∂t{displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} }{partial t}},!}、（2）

∇⋅B=0{displaystyle nabla cdot mathbf {B} =0,!}、（3）

∇×B=μ0ϵ0∂E∂t{displaystyle nabla times mathbf {B} =mu _{0}epsilon _{0}{frac {partial mathbf {E} }{partial t}},!}；（4）

其中，E{displaystyle mathbf {E} ,!}是電場，B{displaystyle mathbf {B} ,!}是磁場，ϵ0{displaystyle epsilon _{0},!}是真空電容率，μ0{displaystyle mu _{0},!}是真空磁導率。

滿足上述條件的一個解是E=B=0{displaystyle mathbf {E} =mathbf {B} =mathbf {0} ,!}，然而這是一個平庸解，並沒有甚麼有意思的物理意義。若想得到有意思的解答，必須稍做一些運算。取公式（2）的旋度，

∇×(∇×E)=∇×(−∂B∂t){displaystyle nabla times left(nabla times mathbf {E} right)=nabla times left(-{frac {partial mathbf {B} }{partial t}}right),!}。（5）

應用一個向量恆等式，再將公式（1）代入，則可得到：

∇×(∇×E)=∇(∇⋅E)−∇2E=−∇2E{displaystyle nabla times left(nabla times mathbf {E} right)=nabla left(nabla cdot mathbf {E} right)-nabla ^{2}mathbf {E} =-nabla ^{2}mathbf {E} ,!}。（6）

應用公式（4），公式（5）右邊變為

∇×(−∂B∂t)=−∂∂t(∇×B)=−μ0ϵ0∂2E∂t2{displaystyle nabla times left(-{frac {partial mathbf {B} }{partial t}}right)=-{frac {partial }{partial t}}left(nabla times mathbf {B} right)=-mu _{0}epsilon _{0}{frac {partial ^{2}mathbf {E} }{partial t^{2}}},!}。（7）

將公式（6）和（7）代回公式（5），可以得到電場的波動方程式：

∇2E=μ0ϵ0∂2E∂t2{displaystyle nabla ^{2}mathbf {E} =mu _{0}epsilon _{0}{frac {partial ^{2}mathbf {E} }{partial t^{2}}},!}。

使用類似的方法，可以得到磁場的波動方程式：

∇2B=μ0ϵ0∂2B∂t2{displaystyle nabla ^{2}mathbf {B} =mu _{0}epsilon _{0}{frac {partial ^{2}mathbf {B} }{partial t^{2}}},!}。

這兩個方程式就是真空的電磁波方程式，描述傳播於真空的電磁波。更簡易地表達，

◻E=0{displaystyle Box mathbf {E} =0,!}、

◻B=0{displaystyle Box mathbf {B} =0,!}；

其中，◻=∇2−1v02∂2∂t2{displaystyle Box =nabla ^{2}-{frac {1}{{v_{0}}^{2}}}{frac {partial ^{2}}{partial t^{2}}},!}是達朗白算符，v0=1μ0ϵ0{displaystyle v_{0}={frac {1}{sqrt {mu _{0}epsilon _{0}}}},!}是波動傳播的速度。

在自由空間裏，v0{displaystyle v_{0},!}是光速c{displaystyle c,!}。馬克士威方程組連結了三個基本物理量：真空電容率ϵ0{displaystyle epsilon _{0},!}、真空磁导率μ0{displaystyle mu _{0},!}和光速c{displaystyle c,!}。这组关系是在麦克斯韦的电动力学发展之前就由威廉·爱德华·韦伯与鲁道夫·科尔劳施发现，但麦克斯韦是首个创造与波在光速传播相一致的场论的人。

前面已經找到了兩個方程式。但是馬克士威方程組有四個方程式，所以，還有很多重要的訊息隱藏在這个方程式裏。思考一個一般的電場向量波動的解，

E=E0f(k⋅r−ωt){displaystyle mathbf {E} =mathbf {E} _{0}fleft(mathbf {k} cdot mathbf {r} -omega tright),!}；

其中，E0{displaystyle mathbf {E} _{0},!}是常數振幅，f(...){displaystyle f(...),!}是任意二次可微函數，k{displaystyle mathbf {k} ,!}是波向量，r0{displaystyle mathbf {r} _{0},!}是位置向量，ω{displaystyle omega ,!}是角頻率。

波動方程式◻f=0{displaystyle Box mathbf {f} =0,!}的通解是f(k⋅r−ωt){displaystyle fleft(mathbf {k} cdot mathbf {r} -omega tright),!}。也就是說，

∇2f(k⋅r−ωt)=1c02∂2∂t2f(k⋅r−ωt){displaystyle nabla ^{2}fleft(mathbf {k} cdot mathbf {r} -omega tright)={frac {1}{{c_{0}}^{2}}}{frac {partial ^{2}}{partial t^{2}}}fleft(mathbf {k} cdot mathbf {r} -omega tright),!}。

將電場的公式代入公式（1）：

∇⋅E=k⋅E0f′(k⋅r−ωt)=0{displaystyle nabla cdot mathbf {E} =mathbf {k} cdot mathbf {E} _{0}f'left(mathbf {k} cdot mathbf {r} -omega tright)=0,!}。

只要電場垂直於波向量（波動傳播的方向），這函數形式的電場必定滿足馬克士威方程組：

E⋅k=0{displaystyle mathbf {E} cdot mathbf {k} =0,!}。

再將電場的公式代入公式（2）：

∇×E=k^×E0f′(k⋅r−ωt)=−∂B∂t{displaystyle nabla times mathbf {E} ={hat {mathbf {k} }}times mathbf {E} _{0}f'left(mathbf {k} cdot mathbf {r} -omega tright)=-{frac {partial mathbf {B} }{partial t}},!}。

所以，電場與其對應磁場的關係為：

B=1ωk×E{displaystyle mathbf {B} ={frac {1}{omega }}mathbf {k} times mathbf {E} ,!}。

在自由空間內，電磁波不只是有以光速傳播的性質，電磁波的電場部分和磁場部分有特定的相對定向、相對大小。它們之間的相位一樣。電場，磁場，波動傳播的方向，都互相垂直於對方。波動傳播的方向是E×B{displaystyle mathbf {E} times mathbf {B} ,!}。

從電磁波傳播的方向看去，電場或許是以上下的方式震盪，而磁場以左右的方式震盪。但若將這圖樣旋轉90度，則電場以左右的方式震盪，而磁場以上下的方式震盪，而波動傳播的方向仍舊相同。這是波動方程式的另一種解答。對於波動同樣傳播的方向，這定向的任意性現象稱為偏振^[7]。

參見

参考文献

外部链接

• Clemson University的網頁：Electromagnetic Radiation。


• 
  Project PHYSNET的網頁： Electromagnetic Waves from Maxwell's Equations 。

查 论 编 电磁学 靜電學 電荷 電場 導體 絕緣體 摩擦起電效應 静电放电 静电感应 库仑定律 高斯定律 电通量 电势能 电偶极矩 電極化 電位移 靜磁學 安培定律 磁場 磁化强度 磁通量 毕奥-萨伐尔定律 磁矩 高斯磁定律 磁矢勢 电动力学 洛伦兹力 電磁感應 法拉第电磁感应定律 楞次定律 位移電流 馬克士威方程組 电磁场 电磁波 馬克士威應力張量 坡印廷向量 黎納-維謝勢 傑斐緬柯方程式 渦電流 倫敦方程 推遲勢 自由空間 电路 电流 電勢 電壓 电阻 欧姆定律 串聯電路 並聯電路 直流電 交流電 带电流 中性流 電動勢 電容 电感 阻抗 电导 波导 憶阻器 基爾霍夫電路定律 協變表述 電磁張量 四維電流密度 電磁應力-能量張量 四維勢 发展史 庫侖 安培 高斯 奧斯特 亨利 法拉第 馬克士威 黑維塞 韋伯 特斯拉 勞侖茲 赫茲 伏打