Rearuh

沿著自轉軸轉動的球體

轉動，是指物件旋轉的運動。三維物件繞著旋轉的軸稱為轉動軸或旋轉軸，若旋轉軸通過物體的質心，則稱此物體在自轉^[1]，而此軸稱為自轉軸。

恆星和行星都會自轉，小天體亦大多會自轉。作為天體的集合體，星系也會自轉^[2]。

如果行星自轉軸在長期運動中漸漸偏離原有方向，即會產生歲差^[3]。

數學

在三維的空間中，轉動以物體繞著轉動軸作旋轉表示。假若此物體的轉動軸是在物體的內部，則此物體繞自己旋轉；這就表示其角動量的值會受其相對速度或是此物體是否為不受力的自由運動而決定。

數學中的轉動

轉動為保持固定繞一點旋轉的剛體運動，不同於移動。這一定義可應用在兩維及三維空間（平面和空間上的分別）。三維空間的旋轉為保持在固定的一條線作旋轉，即三維空間的轉動是繞一個軸旋轉。此從歐拉旋轉定理而來。所有的剛體旋轉運動其運動狀態可能是轉動、移動、或轉動加移動所造成^[4]。

轉動簡單說為一對於共同點的徑向漸進運動，其共同點位於運動轉軸上，轉軸與運動平面之間夾90度角互相垂直。若轉軸位於物體自身外則稱為軌道運動，例如：地球相對於太陽的公轉^[2]。轉動和軌道運動或者是自轉主要的差異僅為轉軸位於物體自身的內或外。而此差異可以在討論剛體時說明。若此轉動為兩個圍繞相同的點/軸的轉動的第三個轉動結果，則此逆向轉動的結果也是相同。因此，上述一系列的轉動，在數學上稱作“群”。然而，繞旋轉點/軸和繞另一個點或軸轉動可能會導致其他的旋轉，例如移動^[5]。

慣性座標的轉動為沿著x、y和z軸的旋轉運動。在空間中轉動的結果可利用繞x軸、y軸及z軸旋轉來表示，這就是說，任何空間的旋轉運動可以分解成各個分量旋轉運動之結合。在飛行動力學上，轉動的座標軸為偏航、俯仰和滾動（稱為Tait-Bryan angles）。這些座標軸也用於電腦繪圖^[6]。

天文學

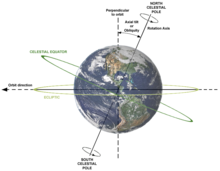
地球的自轉

在天文學中，轉動是一種普遍觀察到的現象。恆星、行星和類似星體皆繞著自轉軸旋轉，第一次測得太陽系中的行星旋轉速率是以視覺特徵量測得到。而星體的轉動主要是以都普勒頻移或觀察表面活動特徵方式量測^[2]。

在地球的參考座標中，這種轉動產生的離心加速度會些微的抵銷重力，所產生的影響之一是物體在赤道的重量會稍微少一點，另一個則是地球會略微變成一個橢圓球體^[7]。

行星的旋轉所造成的另一效應為進動現象，如同陀螺儀一般，行星自轉軸會有些微的擺動，但要千年才能觀察到此角度變化，而目前地球自轉軸與其軌道平面（黃道面）的夾角為23.45度^[8]。

自轉與公轉

月球的公轉

許多領域裡，轉動（公轉）常當作旋轉的同義詞，特別是天文學以及相關領域。為了更清楚的描述一物體繞著另一物體旋轉而以公轉一詞稱軌道公轉，而自轉則指繞某一特定軸旋轉^[9]。

衛星繞行星公轉，行星繞恆星公轉（如地球繞太陽），恆星緩慢的繞著星系中心公轉，而星系的運動相當複雜，但其都包含公轉分量^[10]。

轉動簡單說為一對於共同點的徑向漸進運動，其共同點位於運動轉軸上，轉軸與運動平面之間夾90度角互相垂直。若轉軸位於物體自身外，則稱為軌道運動。轉動和軌道運動或者是自轉，絲毫沒有差異，主要的差異僅為轉軸位於物體自身的內或外。而此差異可以在討論剛體時說明^[11]。

逆向自轉

我們的太陽系中多數行星包括地球，繞太陽運動時自轉方向皆與公轉方向相同，但金星和天王星例外，目前的推測是天王星一開始的自轉方向也與其他行星相同，但在宇宙早期遭到側面的撞擊而使自轉軸翻轉，而金星則被認為是緩慢的向後旋轉（或上下倒置），另外矮行星冥王星（原被視為行星）則為不同於上述情形的異常情況^[12]。

物理

轉動的速度以角頻率（弧度/秒）或頻率（轉 /秒，轉 /分），或週期（秒，天，等...）來表示。角頻率的時間變化率是角加速度（弧度/秒²），此變化為扭矩所造成。扭矩與角加速度的比值為轉動慣量。
角速度向量同時也能描述旋轉軸的方向。同樣地扭矩也是以向量表示^[13]。

根據右手定則，角動量的方向指向觀察者則角速度方向為逆時針，反之則為順時針，例如：螺旋運動^[14]。

轉動簡單說為一對於共同點的徑向漸進運動，其共同點位於運動轉軸上，轉軸與運動平面之間夾90度角互相垂直。若轉軸位於物體自身外，則稱為軌道運動。轉動和軌道運動或者是自轉，絲毫沒有差異，主要的差異僅為轉軸位於物體自身的內或外。而此差異可以在討論剛體時說明^[15]。

飛行學

飛行動力學中的座標軸

在飛行動力學，轉動的座標軸為俯仰，滾轉和偏航。轉動一詞也用於航空提及向上飛行（鼻翼向上移動）的飛機，特別是應用在開始起飛後爬升^[16]。

遊樂設施

許多娛樂設施的運行都是利用轉動的原理。例如：摩天輪的中央有一個水平軸，平行軸兩端的車廂轉動方向相反。因為重力及機械力，所以在任何時間車廂所受的重力方向是與地面垂直，故車廂不旋轉，只是移動。而其運動的圓周軌跡可由切線平移向量所描述^[17]。旋轉木馬提供了一個垂直的旋轉軸。此遊樂設施結合了許多不同木馬各自的旋轉軸。與旋轉飛機有關的旋轉，機械提供垂直軸，而對水平旋轉軸是由於向心力所造成。在雲宵飛車的橫軸逆旋轉是一個或多個完整的週期，而慣性使人保持在自己的座位^[18]。

運動

轉動在許多運動中扮演重要的角色。網球中的上旋球和下旋球^[19]；撞球的拉竿跟推竿；保齡球及棒球的曲球等^[20]。其中，乒乓球是讓球員利用球拍撞擊球進而旋轉球^[21]。

參見

• 地球自轉


• 自轉週期


• 公轉

參考文獻

參考書目

• 
  Hestenes, David. New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. 1999. ISBN 0-7923-5514-8. 
  

• 
  Lounesto, Pertti. Clifford algebras and spinors. Cambridge: Cambridge University Press. 2001. ISBN 978-0-521-00551-7. 
  

• 
  Brannon, Rebecca M. A review of useful theorems involving proper orthogonal matrices referenced to three-dimensional physical space. (PDF). Albuquerque: Sandia National Laboratories. 2002. 
  

• Andrea Milani and Giovanni F. Gronchi. Theory of Orbit Determination (Cambridge University Press; 378 pages; 2010). Discusses new algorithms for determining the orbits of both natural and artificial celestial bodies.


• Julian Knight, Cricket for Dummies, John Wiley and Sons, 2006