光度
光度在科學的不同領域中有不同的意義。
光度學
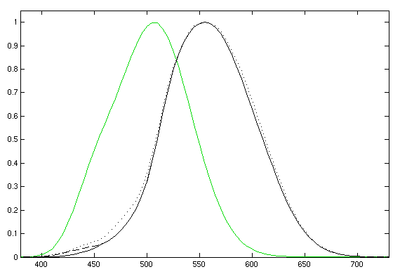
黑色曲线为亮适应光度函数曲线,绿色曲线为暗适应光度函数曲线。实线为CIE 1931标准。断续线为1978年修正数据。点线为2005年修正数据。横坐标单位为nm。
在光度学(photometry)中,"光度"(luminosity)经常与亮度(luminance)弄混。亮度(luminance)是光源在给定方向上单位面积单位立体角内所发出的的光通量,单位是尼特。光度(luminosity)并不是一个物理量,这个词用于光度函数。
光度也指发光强度(Luminous intensity)。
人眼能相当精确地判断两种颜色的光亮暗感觉是否相同。所以为了确定眼睛的光谱响应,可将各种波长的光引起亮暗感觉所需的辐射通量进行比较。在较明亮环境中人的视觉对波长为555.016nm的绿色光最为敏感。设任意波长为λ{displaystyle lambda }


- V(λ)=Ψ555.016Ψλ{displaystyle V(lambda )={frac {Psi _{555.016}}{Psi _{lambda }}}}
叫做光度函数(luminosity function)或视见函数(visual sensitivity function)。例如,实验表明,1mW的555.0nm绿光与2.5W的400.0nm紫光引起的亮暗感觉相同。于是在400.0nm的光度函数值为
- V(400.0nm)=10−32.5=0.0004.{displaystyle V(400.0nm)={frac {10^{-3}}{2.5}}=0.0004.}
衡量光通量的大小,要以光度函数为权重把辐射通量折合成对人眼的有效数量。对波长为λ{displaystyle lambda }


- Φv=Kmax∫V(λ)ψ(λ)dλ{displaystyle Phi _{v}=K_{max}int V(lambda )psi (lambda )dlambda }
式中Kmax{displaystyle K_{max}}
天文學
在天文學中,光度(luminosity)是物體每單位時間內輻射出的總能量,即辐射通量,在國際單位制是瓦特(Watt),在厘米克秒制中是“爾格/秒”,天文学常以太陽光度來表示。L⨀{displaystyle L_{bigodot }}
光度是與距離無關的物理量,而人眼观看到的天体的亮度(实际上是照度)則明顯的與距離有關,而且是與距離的平方成反比,通常會以視星等來量度。
在測量恆星的亮度時,光度、視星等和距離是相關的參數。如果你已經知道其中的兩項,就可以算出第三項。因為太陽的光度是一個標準值,以太陽的視星等和距離做為這些參數的比較標準,就很容易完成彼此之間的轉換。
光度和亮度之間的計算

點光源S向所有的方向輻射光線。穿越面積A的總量會隨著與光源的距離改變而改變。
假設L{displaystyle L}

b=LA{displaystyle b={frac {L}{A}}}




曾經說明過恆星的光度L{displaystyle L}


L=4πR2σT4{displaystyle L=4pi R^{2}sigma T^{4}}
除以太陽光度L⨀{displaystyle L_{bigodot }}
LL⨀=(RR⨀)2(TT⨀)4{displaystyle {frac {L}{L_{bigodot }}}={left({frac {R}{R_{bigodot }}}right)}^{2}{left({frac {T}{T_{bigodot }}}right)}^{4}}
對一顆主序星,光度也與質量相關:
LL⨀∼(MM⨀)3.9{displaystyle {frac {L}{L_{bigodot }}}sim {left({frac {M}{M_{bigodot }}}right)}^{3.9}}
這就很容易知道恆星的光度、溫度、半徑和質量之間都是有關聯的。
恆星的星等與亮度間是對數的關係,視星等是從地球上觀察到的亮度,絕對星等是在10秒差距上的視星等。
只要知道光度,我們就可以計算在任一給定距離上的視星等:
- mstar=msun−2.5log10(LstarL⨀⋅(rsunrstar)2){displaystyle m_{rm {star}}=m_{rm {sun}}-2.5log _{10}left({L_{rm {star}} over L_{bigodot }}cdot left({frac {r_{rm {sun}}}{r_{rm {star}}}}right)^{2}right)}
,此處
mstar是恆星的視星等(一個純數字)
msun是太陽的視星等(也是一個純數字)
Lstar是恆星的光度
L⨀{displaystyle L_{bigodot }}
rstar是到恆星的距離
rsun是到太陽的距離
很簡單的,讓msun = −26.73,rsun = 1.58 × 10−5 光年:
- mstar = − 2.72 − 2.5 · log(Lstar/diststar2)
例如:
天狼星的光度是多少?
- 天狼星的距離是8.6光年,星等為−1.47。
- Lum(天狼星) = 0.0813 · 8.62 · 10−0.4·(−1.47) = 23.3 × L⨀{displaystyle L_{bigodot }}
- 我們可以說天狼星的光度是太陽的23倍,或是它輻射出23倍太陽光度的能量。
一顆熱星等為−10的明亮恆星的光度是106L⨀{displaystyle L_{bigodot }}





