Rearuh

地球附近重力加速度随距地高度的变化

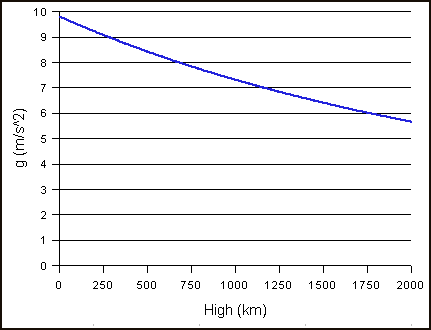
重力加速度是一個物體仅受重力作用的情況下所具有的加速度。重力加速度會隨高度增加而下降。

假設一個質量為m的質點與一質量為M的均勻球體的距離為r時，質量所受的重力大小為：

F=GMmr2{displaystyle F=G{Mm over r^{2}}}

其中G為重力常數。
根据牛頓第二定律

F=mag{displaystyle F=ma_{g}!}

可得重力加速度為

ag=GMr2{displaystyle a_{g}=G{M over r^{2}}}，与质量m无关。

地球表面的重力加速度

g的單位是加速度的单位，而不是力的單位。在地球表面附近，一質點的自由落體加速度g與它的重力加速度a稍微不同，一個質點的重量mg與它所受的重力（地球万有引力）也不同，原因是地球會自轉。若考慮地球自轉，則：

（測量到的重量mg）=（重力的大小ma）-（質量m×向心加速度w²R）

可以得到：

（自由落體加速度g）=（重力加速度a）-（向心加速度w²R）

注意以上式子中的减法为矢量相减。自由落體加速度實際上是小於重力加速度的，方向也略有区别，在赤道上則相差最多，但由於地球的半徑與自轉週期的關係，兩者大約只相差0.034m/s²，因此在日常使用的計算上，重量與重力之間的差異通常可以忽略，但若做為精密飛行器的計算，則需要考慮進去。

地表附近的所有物體下降的加速度都介於9.78和9.83m/s²之間，差別是取決於緯度等因素（赤道最少，南北極最大），標準重力加速度是9.80665 m/s²（為方便計算，一般使用9.81 m/s²、9.8 m/s²或10 m/s²）。

近似公式

根据地球参考椭球，可以导出在地理纬度φ{displaystyle varphi } 海拔高度h{displaystyle h}的重力加速度近似值：
^[1]

g ≈ g0 (1+0.0052884sin2⁡φ−0.0000059sin2⁡2φ)−0.000003086h{displaystyle g approx g_{0} (1+0.0052884sin ^{2}varphi -0.0000059sin ^{2}2varphi )-0.000003086h}

（注：原书sin2{displaystyle sin ^{2}}为sin{displaystyle sin }，疑为笔误）

其中g0≈9.78046 m/s2{displaystyle g_{0}approx 9.78046 m/s^{2}}为赤道海平面上的重力加速度。

有的书会给出稍微不同的表达式：
^[2][3]

g(h=0) ≈ 9.780318 (1+5.3024×10−3sin2⁡φ−5.9×10−6sin2⁡2φ)m/s2{displaystyle g(h=0) approx 9.780318 (1+5.3024!times !10^{-3}sin ^{2}varphi -5.9!times !10^{-6}sin ^{2}2varphi )quad m/s^{2}}

dg(h=0)dh ≈ −3.0877×10−6 (1−1.39×10−3sin2⁡φ)m/s2/m{displaystyle {frac {mathrm {d} g(h=0)}{mathrm {d} h}} approx -3.0877!times !10^{-6} (1-1.39!times !10^{-3}sin ^{2}varphi )quad m/s^{2}/m}

其中h=0{displaystyle h=0}表示在海平面上。对重力精度要求不高时，可以采用下式计算不同高度的重力：

g(h)=g(h=0)/(1+h/R0)2{displaystyle g(h)=g(h=0)/(1+h/R_{0})^{2}}

其中R0≈6371 km{displaystyle R_{0}approx 6371 km}是地球的平均半径。

參見

• 地球引力


• 牛頓運動定律


• 空氣阻力


• 標準重力


• 重力火車

資料來源

• Fundamentals of Physics 8/E Extended ISBN 9780470046180
  


• 物理学基础ISBN 7-111-15715-X/O·390(课) page323