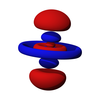
d軌域
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
在化學與原子物理學中,d軌域(英语:d orbital)是一種原子軌域,其角量子數為2,磁量子數可以為0、±1、±2,且每個殼層裡有五個d軌域,共可容下10個電子。
d軌域是很常見的軌域,大部分的過渡金屬的價軌域都是d軌域,在同一個主量子數中,d軌域是能量第三低的軌域,比s軌域與p軌域來的高,由於能階交錯,若以週期的角度來看,第4、5週期中,在價殼層中的d軌域能量很低,僅次於同一個價殼層中的s軌域。但第六週期出現能量更低的f軌域。
另外,d軌域可以和s軌域與p軌域發生混成形成dsp混成軌域[1][2]。
目录
1 命名
2 結構
3 電子波
4 能階交錯
5 性質
6 d軌域
7 d區元素
8 參考文獻
8.1 引用
8.2 书籍
9 參見
命名
d軌域的「d」是「diffused」,其為「漫系光譜」之意。
結構

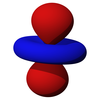
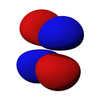
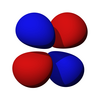
五種d軌域的形狀,除了dz2之外,其他四個形狀相同,只是方向不同

5d軌域模型,紅色和藍色中間空隙則為波節
d軌域從主量子數n=3開始出現,最小的d軌域是3d軌域,也就是說1d、2d軌域不存在,當角量子數為2時,其軌域為d軌域,主量子數不可小於三,對應於五個磁量子數2、1、0、-1、-2,在3d軌域中,有五個能量相同的3d軌域,同樣的,主量子數為4以上時也有五個4d軌域,因此,每個殼層都有五個d軌域,它們分別為dz2、dx2-y2、dxy、dyz、dxz,但是沒有dx2、dy2、dy2-z2、dx2-z2。在存在的五個d軌域(dz2、dx2-y2、dxy、dyz、dxz)中,有四個形狀相同,分別為:dx2-y2、dxy、dyz、dxz但方向不同,而dz2是五個d軌域中形狀與眾不同的一個,儘管如此,dz2軌域仍具有和dx2-y2、dxy、dyz及dxz相同之能量。
4d、5d、6d軌域可視為性質與3d軌域相似,只是大小比較大,其與p軌域類似,也有「正負性」,這些「正負性」變化在原子軌域彼此形成化學鍵時非常重要。
d軌域一樣有波節面,類似於p軌域的形式,但dz2軌域中間的部分較特別,是一個環狀結構像外的波,但電子出現概率和s軌域相反,例如4dz2軌域的中間部分:在靠近原子核之處電子出現概率幾乎是0,然後開始增加,出現一個較高電子出現概率的環狀區域,但繼續向外看之後,隨即降為0,接著又增加,出現一個更大的較高電子出現概率的環狀區域,然後在距離原子核甚遠的地方又為0,而上下的雙啞鈴形的結構則與p軌域相同。
電子波
5個d軌域的角量子數ℓ=2。角部分的d軌道經常會表示為:
- ψn2c(r)=Rn2(r)X2c(r){displaystyle psi _{n2c}(mathbf {r} )=R_{n2}(r)X_{2c}(mathbf {r} )}
的d軌道角部分的三次諧波為X2c(r){displaystyle X_{2c}(mathbf {r} )}
- dz2=N2c3z2−r22r23=Y20{displaystyle d_{z^{2}}=N_{2}^{c}{frac {3z^{2}-r^{2}}{2r^{2}{sqrt {3}}}}=Y_{2}^{0}}
- dxz=N2cxzr2=−12(Y21−Y2−1){displaystyle d_{xz}=N_{2}^{c}{frac {xz}{r^{2}}}=-{frac {1}{sqrt {2}}}left(Y_{2}^{1}-Y_{2}^{-1}right)}
- dyz=N2cyzr2=i2(Y21+Y2−1){displaystyle d_{yz}=N_{2}^{c}{frac {yz}{r^{2}}}={frac {i}{sqrt {2}}}left(Y_{2}^{1}+Y_{2}^{-1}right)}
- dxy=N2cxyr2=−i2(Y22−Y2−2){displaystyle d_{xy}=N_{2}^{c}{frac {xy}{r^{2}}}=-{frac {i}{sqrt {2}}}left(Y_{2}^{2}-Y_{2}^{-2}right)}
- dx2−y2=N2cx2−y22r2=12(Y22+Y2−2){displaystyle d_{x^{2}-y^{2}}=N_{2}^{c}{frac {x^{2}-y^{2}}{2r^{2}}}={frac {1}{sqrt {2}}}left(Y_{2}^{2}+Y_{2}^{-2}right)}
和
- N2c=(154π)1/2{displaystyle N_{2}^{c}=left({frac {15}{4pi }}right)^{1/2}}
| dz2 | dxz | dyz | dxy | dx2-y2 |
|---|---|---|---|---|
 |  |  |  |  |
能階交錯
d軌域有能階交錯現象。例如,3d的能量似乎應該低於4s,而實際上E3d>E4s。按能量最低原理,電子在進入核外電子層時,不是排完3p就排3d,而是先排4s,排完4s才排3d。
性質
d軌域在半填滿和全填滿時較穩定,因此,許多過渡金屬傾向於失去d軌域的電子直到其成為半填滿為止,如鐵,原價電子組態為3d64s2,失去s軌域後還會再放出1個d軌域電子,使其成為Fe3+,組態為:3d5,此時d軌域半填滿,因此Fe3+較穩定,這也是為何Fe2+離子傾向於變成Fe3+離子的原因。
d軌域
在周期表中,過度金屬的價軌域是d軌域,除了內過度金屬,另外,除了前三周期之外,大部分的非金屬的價殼層之d軌域是填滿的。
d區元素
d區元素是指這些元素中具有最高能量的電子是填在d軌域上的,是元素週期表中的副族元素,即第3至第12族元素。这些元素有时也被称作过渡金属。
參考文獻
引用
^ 含有d轨道的杂化作用. 化学键的共价键理论:现代价键理论. 彭军. [2012-01-28] (中文).
^ An example of dsp2 hybridization. Chemical Bonding: Multiple bonds, d orbitals. [2012-01-28]. (原始内容存档于2012-01-18) (英语).
书籍
- 曾國輝《原子結構》建宏出版社 台北市 1999 ISBN 957-724-801-2
參見
- s軌域
- p軌域
- f軌域
- 原子軌域
- d區元素
| ||||||||||||||||||||||||||