Rearuh

階乘，定義于整個實數（負整數除外）。
例如：1!=0!=1{displaystyle 1!=0!=1,}，(−0.5)!=π{displaystyle (-0.5)!={sqrt {pi }}}，0.5!=0.5π.{displaystyle 0.5!=0.5{sqrt {pi }}.}

在數學中，正整数的階乘（英语：factorial）是所有小於及等於該數的正整數的積，計為n!，例如5的階乘計為5!，其值為120：

5!=5×4×3×2×1=120.{displaystyle 5!=5times 4times 3times 2times 1=120,.}

並定義，1的階乘1!為1、0的階乘0!亦為1，其中，0的階乘表示一個空積^[2]。

1808年，基斯頓·卡曼引進這個表示法：n!=∏k=1nk∀n≥1{displaystyle n!=prod _{k=1}^{n}kquad forall ngeq 1}，符號Π{displaystyle Pi }表示連續乘積，亦即n!=1×2×3×...×n。階乘亦可以遞迴方式定義：0!=1，n!=(n-1)!×n。除了自然數之外，階乘亦可定義于整個實數（負整數除外），其与伽瑪函數的关系为：

z!=Γ(z+1)=∫0∞tze−tdt{displaystyle z!=Gamma (z+1)=int _{0}^{infty }t^{z}e^{-t},dt}

階乘應用在許多數學領域中，最常應用在組合學、代數學和数学分析中。在組合學中，階乘代表的意義為n個相異物件任意排列的數量，例如前述例子，5!=120其代表了5個相異物件共有120種排列法。在正整數的情形下，n的階乘又可以稱為n的排列數。

歷史

早在12世紀，印度學者就已有使用階乘的概念來計算排列數的紀錄^[3]。1677年時，法比安·斯特德曼使用Change ringing（英语：Change ringing）來解釋階乘的概念^[5]。在描述遞迴方法之後，斯特德將階乘描述為：「現在這些方法的本質是這樣的：一個數字的變化數包含了所有比他小的數字（包括本身）的所有變化數……因為一個數字的完全變化數是將較小數字的變化數視為一個整體，並透過將所有數字的完整變化聯合起來。」，其原話如下：

Now the nature of these methods is such, that the changes on one number comprehends [includes] the changes on all lesser numbers ... insomuch that a compleat Peal of changes on one number seemeth to be formed by uniting of the compleat Peals on all lesser numbers into one entire body.^[6]

而符號n!是由法國數學家Christian Kramp在1808年使用^[8]。

定義

階乘可透過連乘積來定義：

n!=1⋅2⋅3⋯(n−2)⋅(n−1)⋅n,{displaystyle n!=1cdot 2cdot 3cdots (n-2)cdot (n-1)cdot n,}

用連乘積符號可表示為：

n!=∏i=1ni.{displaystyle n!=prod _{i=1}^{n}i.}

從上述公式中，可以推導出遞歸關係：

n!=n⋅(n−1)!{displaystyle n!=ncdot (n-1)!}

但遞迴定義須給出base case，因此需要定義零的階乘。
除此之外，遞迴關係在皆乘函數中各個值皆成立，例如：

5!=5⋅4!6!=6⋅5!50!=50⋅49!{displaystyle {begin{aligned}5!&=5cdot 4!\6!&=6cdot 5!\50!&=50cdot 49!end{aligned}}}

0的階乘

為了將遞歸關係擴展到n = 0，因此需要定義0的階乘：

0!=1{displaystyle 0!=1}

可以得到

1!=1⋅0!=1.{displaystyle 1!=1cdot 0!=1.}

有幾個獨立的理由認為這個定義是和諧的。 其中包括：

• 在n = 0的情況，n!定義為「沒有任何數字相乘的結果」，所以更廣泛之慣例的例子是以不存在任何因數的乘法單位元素來當作其解。（參閱空積）


• 對於零個物品只有一種排列方式，因為沒有任何東西可以置換，唯一的重新排列就是什麼都不做。


• 它使組合數學中的許多恆等式對所有適用的值皆有效，例如從空集合中選擇0個元素的方法數，可由二項式係數給出：

(00)=1{displaystyle {binom {0}{0}}=1}.

而從空集合中選擇0個元素的方法數為一種，即沒有任何東西可以取，唯一的取法就是什麼都不做。定義0!=1{displaystyle 0!=1}可以滿足：

(00)=0!0!0!=1{displaystyle {binom {0}{0}}={frac {0!}{0!0!}}=1}.

更一般地，在n個相異元素的集合中取出n個相異元素的方法數，可由二項式係數給出：

(nn)=1{displaystyle {binom {n}{n}}=1}.

其方法數只有一種，即全部取出。定義0!=1{displaystyle 0!=1}可以滿足：

(nn)=n!n!0!=1{displaystyle {binom {n}{n}}={frac {n!}{n!0!}}=1}

• 此定義允許將許多公式更嚴謹地表達為冪級數，例如指數函數：

ex=∑n=0∞xnn!.{displaystyle e^{x}=sum _{n=0}^{infty }{frac {x^{n}}{n!}}.}

性質

n!可质因子分解为∏p≤np∑r=1n[npr]{displaystyle prod _{pleq n}p^{sum _{r=1}^{n}[{frac {n}{p^{r}}}]}}，如6!=2⁴×3²×5¹。^[9]

計算

階乘與斯特靈公式

@media all and (max-width:720px){body.skin-minerva .mw-parser-output div.mw-graph{min-width:auto!important;max-width:100%;overflow-x:auto;overflow-y:visible}}

n!{displaystyle n!}（藍色）、2πn(ne)n{displaystyle {sqrt {2pi n}}left({frac {n}{e}}right)^{n}}（橘色），數字越大2πn(ne)n,{displaystyle {sqrt {2pi n}}left({frac {n}{e}}right)^{n},}會越趨近n!{displaystyle n!}。但2πn(ne)n{displaystyle {sqrt {2pi n}}left({frac {n}{e}}right)^{n}}在負值則會因為出現虛數而無法使用。

計算n!時，當n不太大時，普通的科學計算機都可以計算，能夠處理不超過10100{displaystyle 10^{100}}數值的計算機可以計算至69!。

當n很大時，可以用斯特林公式估計：
n!≈2πn(ne)n{displaystyle n!approx {sqrt {2pi n}};left({frac {n}{e}}right)^{n}}

更精确的估计是：
n!=2πn(ne)neλn{displaystyle n!={sqrt {2pi n}};left({frac {n}{e}}right)^{n}e^{lambda _{n}}}

其中
112n+1<λn<112n{displaystyle {frac {1}{12n+1}}<lambda _{n}<{frac {1}{12n}}}

部分函數值

非正整數的擴展

階乘原始的定義是在整數，為離散，然而在部分領域如機率論要探討到連續或其他需求（如組合數當取出的數量大於原有的數量會出現負階乘）時，則需要將階乘從正整數推廣到實數，甚至是複數。

Γ函数和Π函数

伽馬函數將階乘函數為非整數插值。主要線索是階乘函數的遞歸關係在連續的伽馬函數中也存在。

除了非負整數之外，還可以為非整數值定義階乘函數，但這需要使用更高級的數值分析方法。

可以透過插值的方式將階乘兩整數之間填入數值，但其插入的數值必須也要滿足階乘的遞迴定義。一個良好的插值結果是Γ函数，其為所有非負整數和複數給出了定義，而當z的實部為正時，可以透過下列瑕積分來計算Γ函数值：

Γ(z)=∫0∞tz−1e−tdt.{displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt,.}

它與階乘的關係是對於任何自然數n滿足：

n!=Γ(n+1).{displaystyle n!=Gamma (n+1),.}

複數的階乘

複數階乘之模與輻角的等值線

可以透過Γ函數來計算複數的階乘。右圖顯示了複數階乘之模與輻角的等值線

令f為：

f=ρeiφ=(x+iy)!=Γ(x+iy+1){displaystyle f=rho e^{ivarphi }=(x+{rm {i}}y)!=Gamma (x+iy+1)}

右圖顯示了幾個模（絕對值）ρ與輻角φ的幾個等級，圖表的繪製範圍為−3 ≤ x ≤ 3, −2 ≤ y ≤ 2個單位長。較粗的鉛直線為輻角值為φ = ±π的等值線。

細線表示模或輻角相等之函數值的位置。在每個負整數的位置為奇點，無法定義其模和輻角，並且在離奇點越近的地方，等值線的密度就越密集。

在|z| < 1時，可使用泰勒級數來計算：

z!=∑n=0∞gnzn.{displaystyle z!=sum _{n=0}^{infty }g_{n}z^{n},.}

其泰勒級數的前幾項係數為：

其中，γ為歐拉-馬斯刻若尼常數

ζ(z)為黎曼ζ函數

部分計算機代數的系統存在可以直接產生這些展開式係數的語法，例如SageMath。

此種方式甚至可以將階乘推廣至四元數甚至其他數學結構。

z	z!
實數
1、2、3、4、5	1、2、6、24、120 （OEIS中的数列A000142）
12{displaystyle {frac {1}{2}}}	π2≈{displaystyle {frac {sqrt {pi }}{2}}approx ,}0.88622692545276{displaystyle 0.88622692545276} （OEIS中的数列A019704）
複數
i{displaystyle i}	0.49801566811836−0.15494982830181i{displaystyle 0.49801566811836-0.15494982830181i} （OEIS中的数列A212877）、（OEIS中的数列A212878）
2i{displaystyle 2i}	0.15190416419017+0.019804630236207i{displaystyle 0.15190416419017+0.019804630236207i}
1+i{displaystyle 1+i}	0.65296549642017+0.34306583981655i{displaystyle 0.65296549642017+0.34306583981655i}
四元數
j{displaystyle j}	0.49801566811836−0.15494982830181j{displaystyle 0.49801566811836-0.15494982830181j}
k{displaystyle k}	0.49801566811836−0.15494982830181k{displaystyle 0.49801566811836-0.15494982830181k}
1+i+j{displaystyle 1+i+j}	0.31694392956467−0.045151372272429i−0.045151372272429j{displaystyle 0.31694392956467-0.045151372272429i-0.045151372272429j}

階乘的色相環複變函數圖形。顏色越深代表絕對值越接近零；顏色越接近白色代表絕對值趨於無窮。其中紅色為正實數、青藍色為負實數。

較大的階乘值可透過双伽玛函数積分的連續分數來近似，這個方法由T. J. Stieltjes於1894提出。

將階乘寫為z! = e^P(z)，其中P(z)為：

P(z)=p(z)+ln⁡2π2−z+(z+12)ln⁡(z),{displaystyle P(z)=p(z)+{frac {ln 2pi }{2}}-z+left(z+{tfrac {1}{2}}right)ln(z),,}

Stieltjes給出了其連分數值：

p(z)=a0z+a1z+a2z+a3z+⋱{displaystyle p(z)={cfrac {a_{0}}{z+{cfrac {a_{1}}{z+{cfrac {a_{2}}{z+{cfrac {a_{3}}{z+ddots }}}}}}}}}

前幾項係數a_n為^[10]：

n	an
0	1/12
1	1/30
2	53/210
3	195/371
4	22,999/22,737
5	29,944,523/19,733,142
6	109,535,241,009/48,264,275,462

負整數的階乘

負整數的階乘可透過階乘的遞迴定義n! = n × (n − 1)!逆推而得：

(n−1)!=n!n.{displaystyle (n-1)!={frac {n!}{n}}.}

但由於計算負一階乘會出現除以零，因此無法直接給出負整數的階乘。

其他數學結構的階乘

透過伽瑪函數或其展開式亦可以將階乘擴展到其他能定義加法和乘法等基本運算的數學結構，如矩陣^[11]。

矩陣的階乘具有如下性質：

A!=Γ(A+I)=AΓ(A)=A(A−I)!{displaystyle A!=Gamma (A+I)=AGamma (A)=A(A-I)!}。

並且Γ(I)=I{displaystyle Gamma (I)=I}，其中，I{displaystyle I}是單位矩陣、A{displaystyle A}是一個方陣，同時A!{displaystyle A!}是一個非奇異矩陣^[12]。

換句話說，即矩陣A{displaystyle A}為單位矩陣的純量n{displaystyle n}倍，其階乘為A!=(nI)!=n!I{displaystyle A!=(nI)!=n!I}，例如(n00n)!=n!I=(n!00n!){displaystyle {bigl (}{begin{smallmatrix}n&0\0&nend{smallmatrix}}{bigr )}!=n!I={bigl (}{begin{smallmatrix}n!&0\0&n!end{smallmatrix}}{bigr )}}

對於一個可對角化矩陣(abcd){displaystyle {bigl (}{begin{smallmatrix}a&b\c&dend{smallmatrix}}{bigr )}}其階乘為：

(abcd)!=Γ((a+1bcd+1))=12Ω(Γ(λ1)(d−a+Ω)+Γ(λ2)(a−d+Ω)−2b(Γ(λ1)−Γ(λ2))−2c(Γ(λ1)−Γ(λ2))Γ(λ1)(a−d+Ω)+Γ(λ2)(d−a+Ω)){displaystyle left.{begin{pmatrix}a&b\c&dend{pmatrix}}right.!=Gamma left({bigl (}{begin{smallmatrix}a+1&b\c&d+1end{smallmatrix}}{bigr )}right)={frac {1}{2Omega }}{begin{pmatrix}Gamma (lambda _{1})left(d-a+Omega right)+Gamma (lambda _{2})left(a-d+Omega right)&-2bleft(Gamma (lambda _{1})-Gamma (lambda _{2})right)\-2cleft(Gamma (lambda _{1})-Gamma (lambda _{2})right)&Gamma (lambda _{1})left(a-d+Omega right)+Gamma (lambda _{2})left(d-a+Omega right)end{pmatrix}}}^[12]

其中，λ1{displaystyle lambda _{1}}和λ2{displaystyle lambda _{2}}是(a+1bcd+1){displaystyle {bigl (}{begin{smallmatrix}a+1&b\c&d+1end{smallmatrix}}{bigr )}}的特徵值，分別為λ1=1+(a+d−Ω)2{displaystyle lambda _{1}=1+{begin{smallmatrix}{frac {left(a+d-Omega right)}{2}}end{smallmatrix}}}和λ2=1+(a+d+Ω)2{displaystyle lambda _{2}=1+{begin{smallmatrix}{frac {left(a+d+Omega right)}{2}}end{smallmatrix}}}，其中，Ω=(a−d)2+4bc{displaystyle Omega ={begin{smallmatrix}{sqrt {(a-d)^{2}+4bc}}end{smallmatrix}}}^[12]

變化

定义扩展

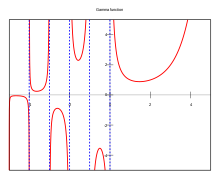
伽瑪函數

階乘的定義可推廣到複數，其与伽瑪函數的关系为：

z!=Γ(z+1)=∫0∞tze−tdt.{displaystyle z!=Gamma (z+1)=int _{0}^{infty }t^{z}e^{-t},mathrm {d} t.!}。

伽瑪函數滿足Γ(n+1)=(n)Γ(n){displaystyle Gamma (n+1)=(n)Gamma (n)}，

另一種定义扩展是阿達馬伽瑪函數，但由於其不在所有實數上皆能滿足階乘的遞迴定義，只有在正整數上滿足階乘的遞迴定義n! = n × (n − 1)!因此比較少被拿出來討論。

H(x+1)=xH(x)+1Γ(1−x){displaystyle H(x+1)=x,H(x)+{frac {1}{Gamma (1-x)}}}

其後面的項1Γ(1−x){displaystyle {frac {1}{Gamma (1-x)}}}只有在正整數的情形為零。也因為其有加上一項，也因此，此擴展在描述負階乘時不會有除以零的情況，而使阿達馬伽瑪函數是一個處處連續、無奇點的函數。

遞進/遞降階乘

• 遞進階乘：(x)n=xn¯=x(x+1)...(x+n−1){displaystyle (x)_{n}=x^{overline {n}}=x(x+1)...(x+n-1)}
  


• 遞降階乘：xn_=x(x−1)...(x−n+1){displaystyle x^{underline {n}}=x(x-1)...(x-n+1)}
  


• xn¯=(−1)n(−x)n_{displaystyle x^{overline {n}}=(-1)^{n}(-x)^{underline {n}}}

双階乘

n!!{displaystyle n!!}表示双階乘，其定義為：
(2n−1)!!=1×3×5×7×⋯×(2n−1){displaystyle (2n-1)!!=1times 3times 5times 7times cdots times (2n-1)}

(2n)!!=2×4×6×8×⋯×(2n)=2nn!{displaystyle (2n)!!=2times 4times 6times 8times cdots times (2n)=2^{n}n!}

廣義的雙階乘

無視上述定義的n!!因為即使值的N，雙階乘為奇數可擴展到最實數和複數z的注意到，當z是一個正的奇數則：

z!!=z(z−2)⋯(3)=2z−12(z2)(z−22)⋯(32)=2z−12Γ(z2+1)Γ(12+1)=2z+1πΓ(z2+1).{displaystyle z!!=z(z-2)cdots (3)=2^{frac {z-1}{2}}left({frac {z}{2}}right)left({frac {z-2}{2}}right)cdots left({frac {3}{2}}right)=2^{frac {z-1}{2}}{frac {Gamma left({frac {z}{2}}+1right)}{Gamma left({frac {1}{2}}+1right)}}={sqrt {frac {2^{z+1}}{pi }}}Gamma left({frac {z}{2}}+1right),.}

獲得的表達接受一個以上公式(2n+1)!!{displaystyle (2n+1)!!}和(2n−1)!!{displaystyle (2n-1)!!}並表示在條件發生的階乘函數的γ既可以看出（使用乘法定理）等同於一個給定在這裡。

z!!定義為所有複數除負偶數。

使用它的定義，半徑為R的n維超球其體積可表示為：

Vn=2(2π)n−12n!!Rn.{displaystyle V_{n}={frac {2(2pi )^{frac {n-1}{2}}}{n!!}}R^{n}.} n=1,3,5,...

Vn=(π)n2n2!Rn.{displaystyle V_{n}={frac {(pi )^{frac {n}{2}}}{{frac {n}{2}}!}}R^{n}.} n=2,4,6,...

多重阶乘

n!(k){displaystyle n!^{(k)}}被称为n的k重阶乘，定义为：

n!(k)={1, if 0≤n<k;n(n−k)!(k),if n≥k.  {displaystyle n!^{(k)}=left{{begin{matrix}1,qquad qquad &&{mbox{if }}0leq n<k;\n(n-k)!^{(k)},&&{mbox{if }}ngeq k.quad ,end{matrix}}right.}

廣義的多重階乘

能將多重階乘推廣到複數（甚至是四元數）

z!(k)=z(z−k)⋯(k+1)=kz−1k(zk)(z−kk)⋯(k+1k)=kz−1kΓ(zk+1)Γ(1k+1).{displaystyle z!^{(k)}=z(z-k)cdots (k+1)=k^{frac {z-1}{k}}left({frac {z}{k}}right)left({frac {z-k}{k}}right)cdots left({frac {k+1}{k}}right)=k^{frac {z-1}{k}}{frac {Gamma left({frac {z}{k}}+1right)}{Gamma left({frac {1}{k}}+1right)}},.}

四次階乘

所謂的四次阶乘（又称四重阶乘） 不是 n!⁽⁴⁾，而是 (2n)!/n!,前幾個四次階乘為

1, 2, 12, 120, 1680, 30240, 665280, ....

它也等於

2n(2n)!n!2n=2n(2⋅4⋯2n)[1⋅3⋯(2n−1)]2⋅4⋯2n=(1⋅2)⋅(3⋅2)⋯[(2n−1)⋅2]=(4n−2)!(4).{displaystyle {begin{aligned}2^{n}{frac {(2n)!}{n!2^{n}}}&=2^{n}{frac {(2cdot 4cdots 2n)[1cdot 3cdots (2n-1)]}{2cdot 4cdots 2n}}\[8pt]&=(1cdot 2)cdot (3cdot 2)cdots [(2n-1)cdot 2]=(4n-2)!^{(4)}.end{aligned}}}

hyper階乘

hyper階乘（hyperfactorial有時譯作過度階乘）寫作H（n），其定義為：

H(n)=∏k=1nkk=11⋅22⋅33⋯(n−1)n−1⋅nn{displaystyle H(n)=prod _{k=1}^{n}k^{k}=1^{1}cdot 2^{2}cdot 3^{3}cdots (n-1)^{n-1}cdot n^{n}}

hyper階乘和階乘差不多，但產生更大的數。hyper階乘的增長速度卻並非跟一般階乘在大小上相差很遠。
前幾項的hyper階乘為：

1, 4, 108, 27648, 86400000, ... （OEIS中的数列A002109）

超級階乘

1995年，尼爾·斯洛恩和西蒙·普勞夫定義了超級階乘（superfactorial）為首n個階乘的積。即sf(n)=1!×2!×3!×...×n!。一般來說

sf(n)=∏k=1nk!=∏k=1nkn−k+1=1n⋅2n−1⋅3n−2⋯(n−1)2⋅n1.{displaystyle mathrm {sf} (n)=prod _{k=1}^{n}k!=prod _{k=1}^{n}k^{n-k+1}=1^{n}cdot 2^{n-1}cdot 3^{n-2}cdots (n-1)^{2}cdot n^{1}.}

前幾項的超級階乘為：

1, 2, 12, 288, 34560, 24883200, ... （OEIS中的数列A000178）

另一種定義

柯利弗德·皮寇弗在他的書Key to Infinity定義了另一個超級階乘，寫作nS!{displaystyle nmathrm {S} !!!!!;,{!}}（nS!{displaystyle nmathrm {S} !!!!!;,{!}}實際上應該是!和S重疊在一起）：nS!=n(4)n{displaystyle nmathrm {S} !!!!!;,{!}=n^{(4)}n}，⁽⁴⁾表示hyper4，使用高德納箭號表示法即nS!=(n!)↑↑(n!){displaystyle nmathrm {S} !!!!!;,{!}=(n!)uparrow uparrow (n!)}。這個數列：

1S!=1{displaystyle 1mathrm {S} !!!!!;,{!}=1}

2S!=22=4{displaystyle 2mathrm {S} !!!!!;,{!}=2^{2}=4}

3S!=6↑↑6=666666{displaystyle 3mathrm {S} !!!!!;,{!}=6uparrow uparrow 6=6^{6^{6^{6^{6^{6}}}}}}，读作6个6重幂。

4S!=(4!)↑↑(4!)=24↑↑24{displaystyle 4mathrm {S} !!!!!;,{!}=(4!)uparrow uparrow (4!)=24uparrow uparrow 24} = 2424...24{displaystyle {begin{matrix}{24_{}^{24^{{}^{.,^{.,^{.,^{24}}}}}}}\end{matrix}}}，一直写24个24，读作24个24重幂。

質數階乘

質數階乘是所有小於或等於該數且大於或等於2的質數的積，自然數n的質數階乘，寫作n#。

目前質數階乘只能用遞迴方式定義，因為尚未找到一個能用基本函數表示所有質數的函數或一條包含所有質數的曲線

一般情況下質數階乘定義為：

n#=∏i=1π(n)pi=pπ(n)#{displaystyle n#=prod _{i=1}^{pi (n)}p_{i}=p_{pi (n)}#}

其中, π(n)是質數計數函數，小於或等於某個實數n的質數的個數的函數≤n。

自然数阶幂

阶幂也称叠幂或者重幂记作n!{displaystyle n^{!}}（感叹号!写在自然数的右上角），它的定义是将自然数1至n的数由大到小作幂指数重叠排列，数学定义如下：

n!=n(n−1)!=n(n−1)(n−2)...321{displaystyle n^{!}=n^{{(n-1)}^{!}}=n_{}^{(n-1)^{{(n-2)}^{.,^{.,^{.,^{{3}^{{2}^{1}}}}}}}}}

其中n ≥ 1，前几项的重幂数为：

1 , 2 , 9 , 262144 , ... （OEIS中的数列A049384）

第5个重幂数是一个有183231位阿拉伯数字组成的超大自然数^[13][14]，其值約為6.20606987866×10183230{displaystyle 6.20606987866times 10^{183230}}

另外一種定義則是每個阶幂都先取一次階乘：

n!(n−1)!!=n!(n−1)!(n−2)!...3!2!1!{displaystyle n!^{{(n-1)!}^{!}}=n!_{}^{(n-1)!^{{(n-2)!}^{.,^{.,^{.,^{{3!}^{{2!}^{1!}}}}}}}}}

前幾個阶乘阶幂為：

1, 2, 36, 48708493958471199415506599153950129703565945470976, ... （OEIS中的数列A073581）

第5个阶乘阶幂值已大於101050{displaystyle 10^{10^{50}}}^[15][16]，其值約為4.3056×101.01274×1050≈101050.00549705084703{displaystyle 4.3056times 10^{1.01274times 10^{50}}approx 10^{10^{50.00549705084703}}}

二次阶幂：

n!!=n!2=n!(n−1)!(n−2)!...3!2!1!{displaystyle n^{!!}=n^{{!}^{2}}={n^{{!}{(n-1)^{{!}{{(n-2)}^{{!}{{.}^{{.}^{{.}^{3^{{!}{2^{{!}{1^{!}}}}}}}}}}}}}}}}

前幾個二次阶幂為：

1, 2, 81...

第4个阶乘阶幂值已大於10438{displaystyle 10^{438}}，其值約為7.975×10438{displaystyle 7.975times 10^{438}}。

相应地，m次阶幂定义如下：

n!m=n!(m−1)(n−1)!m=n!(m−1)(n−1)!(m−1)(n−2)!(m−1)...3!(m−1)2!(m−1)1!(m−1){displaystyle n^{{!}^{m}}=n^{{!}^{(m-1)}{(n-1)}^{!^{m}}}={n^{{!^{(m-1)}}{(n-1)^{{!^{(m-1)}}{{(n-2)}^{{!^{(m-1)}}{{.}^{{.}^{{.}^{3^{{!^{(m-1)}}{2^{{!^{(m-1)}}{1^{!^{(m-1)}}}}}}}}}}}}}}}}}

其中n，m≥1，且n，m∈Z。

倒數階乘

倒數階乘是指所有小於及等於該數的正整數之倒數的積，其值與階乘的倒數相同：

∏k=1n1k=1n!∀n≥1{displaystyle prod _{k=1}^{n}{frac {1}{k}}={frac {1}{n!}}quad forall ngeq 1}

其無窮級數收斂在e^[17]：

∑n=0∞∏k=1n1k=e{displaystyle sum _{n=0}^{infty }prod _{k=1}^{n}{frac {1}{k}}=e}

考量階乘可以表示為連續的伽瑪函數，則有

∫−1∞dxx!=∫0∞dxΓ(x)≈2.80777024,{displaystyle int _{-1}^{infty }{frac {dx}{x!}},=int _{0}^{infty }{frac {dx}{Gamma (x)}},approx 2.80777024,}

這個值又稱為弗朗桑－羅賓遜常數（英语：Fransén–Robinson_constant）。^[18]

符号史

• 瑞士数学家欧拉（Euler, L.）于1751年用大写字母M{displaystyle M}表示m{displaystyle m}阶乘M=1⋅2⋅3⋅⋯⋅m{displaystyle M=1cdot 2cdot 3cdot cdots cdot m}。


• 意大利数学家鲁菲尼（Ruffini, P.）在1799年出版的方程著述中，用小写字母π{displaystyle pi }表示m{displaystyle m}阶乘。


• 德国数学家高斯（Gauss, C.F）于1818年则用Π(n){displaystyle Pi (n)}表示n阶乘。


• 用符号∣n_{displaystyle {underline {mid n}}}表示n{displaystyle n}阶乘的方法起源于英国，尚不能确定其创始人，1827年，由雅来特（Jarrett）的建议得以流行，现代有时亦用此阶乘符号。


• 现在通用的阶乘符号n!{displaystyle n!}是法国数学家克拉姆（Kramp, C.）于1808年最先提出来的，后经德国数学家、物理学家格奥尔格·欧姆（Ohm, M.）等人的倡议而流行起来，直用到现在。

參見

• 伽瑪函數


• 斯特靈公式


• 階乘倒數


• 阶乘符号


• 排列组合


• 威尔逊定理

註釋

參考文獻