Rearuh

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x.^[1][2] It is denoted by π(x) (unrelated to the number π).

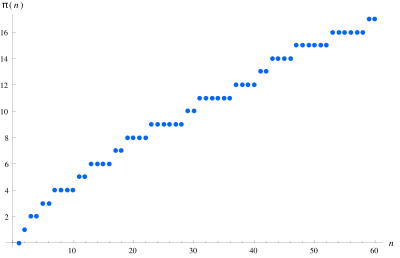
The values of π(n) for the first 60 integers

History

Of great interest in number theory is the growth rate of the prime-counting function.^[3][4] It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately

xln⁡(x){displaystyle {frac {x}{ln(x)}}}

in the sense that

limx→∞π(x)x/ln⁡(x)=1.{displaystyle lim _{xrightarrow infty }{frac {pi (x)}{x/ln(x)}}=1.}

This statement is the prime number theorem. An equivalent statement is

limx→∞π(x)/li⁡(x)=1{displaystyle lim _{xrightarrow infty }pi (x)/operatorname {li} (x)=1!}

where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proofs of the prime number theorem not using the zeta function or complex analysis were found around 1948 by Atle Selberg and by Paul Erdős (for the most part independently).^[5]

More precise estimates of π(x){displaystyle pi (x)!} are now known; for example^{[citation needed]}

π(x)=li⁡(x)+O(xe−ln⁡x/15){displaystyle pi (x)=operatorname {li} (x)+O{bigl (}xe^{-{sqrt {ln x}}/15}{bigr )}!}

where the O is big O notation. For most values of x{displaystyle x} we are interested in (i.e., when x{displaystyle x} is not unreasonably large) li⁡(x){displaystyle operatorname {li} (x)!} is greater than π(x){displaystyle pi (x)!}, but infinitely often the opposite is true. For a discussion of this, see Skewes' number.

Exact form

Of profound importance, if the Riemann hypothesis is true then the prime-counting function equals^{[citation needed]}

π(x)=R⁡(x)−∑ρR⁡(xρ){displaystyle pi (x)=operatorname {R} (x)-sum _{rho }operatorname {R} (x^{rho })}

where

R⁡(x)=∑n=1∞μ(n)nli⁡(x1/n){displaystyle operatorname {R} (x)=sum _{n=1}^{infty }{frac {mu (n)}{n}}operatorname {li} (x^{1/n})},

μ(n) is the Möbius function, li(x) is the logarithmic integral function, and ρ are the complex zeros of the Riemann zeta function which lie along Re(s) = 1/2.

Table of π(x), x / ln x, and li(x)

The table shows how the three functions π(x), x / ln x and li(x) compare at powers of 10. See also,^[3][6][7] and^[8]

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)	x / ln x % Error
10	4	−0.3	2.2	2.500	-7.5%
102	25	3.3	5.1	4.000	13.20%
103	168	23	10	5.952	13.69%
104	1,229	143	17	8.137	11.64%
105	9,592	906	38	10.425	9.45%
106	78,498	6,116	130	12.740	7.79%
107	664,579	44,158	339	15.047	6.64%
108	5,761,455	332,774	754	17.357	5.78%
109	50,847,534	2,592,592	1,701	19.667	5.10%
1010	455,052,511	20,758,029	3,104	21.975	4.56%
1011	4,118,054,813	169,923,159	11,588	24.283	4.13%
1012	37,607,912,018	1,416,705,193	38,263	26.590	3.77%
1013	346,065,536,839	11,992,858,452	108,971	28.896	3.47%
1014	3,204,941,750,802	102,838,308,636	314,890	31.202	3.21%
1015	29,844,570,422,669	891,604,962,452	1,052,619	33.507	2.99%
1016	279,238,341,033,925	7,804,289,844,393	3,214,632	35.812	2.79%
1017	2,623,557,157,654,233	68,883,734,693,281	7,956,589	38.116	2.63%
1018	24,739,954,287,740,860	612,483,070,893,536	21,949,555	40.420	2.48%
1019	234,057,667,276,344,607	5,481,624,169,369,960	99,877,775	42.725	2.34%
1020	2,220,819,602,560,918,840	49,347,193,044,659,701	222,744,644	45.028	2.22%
1021	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	47.332	2.11%
1022	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	49.636	2.02%
1023	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	51.939	1.93%
1024	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	54.243	1.84%
1025	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	56.546	1.77%
1026	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	58.850	1.70%
1027	16,352,460,426,841,680,446,427,399	267,479,615,610,131,274,163,365	508,666,658,006	61.153	1.64%

Graph showing ratio of the prime-counting function π(x) to two of its approximations, x/ln x and Li(x). As x increases (note x axis is logarithmic), both ratios tend towards 1. The ratio for x/ln x converges from above very slowly, while the ratio for Li(x) converges more quickly from below.

In the On-Line Encyclopedia of Integer Sequences, the π(x) column is sequence OEIS: A006880, π(x) − x/ln x is sequence OEIS: A057835, and li(x) − π(x) is sequence OEIS: A057752.

The value for π(10²⁴) was originally computed by J. Buethe, J. Franke, A. Jost, and T. Kleinjung assuming the Riemann hypothesis.^[9]
It was later verified unconditionally in a computation by D. J. Platt.^[10]
The value for π(10²⁵) is due to J. Buethe, J. Franke, A. Jost, and T. Kleinjung.^[11]
The value for π(10²⁶) was computed by D. B. Staple.^[12] All other entries in this table were also verified as part of that work.

Algorithms for evaluating π(x)

A simple way to find π(x){displaystyle pi (x)}, if x{displaystyle x} is not too large, is to use the sieve of Eratosthenes to produce the primes less than or equal to x{displaystyle x} and then to count them.

A more elaborate way of finding π(x){displaystyle pi (x)} is due to Legendre (using the inclusion–exclusion principle): given x{displaystyle x}, if p1,p2,…,pn{displaystyle p_{1},p_{2},ldots ,p_{n}} are distinct prime numbers, then the number of integers less than or equal to x{displaystyle x} which are divisible by no pi{displaystyle p_{i}} is

⌊x⌋−∑i⌊xpi⌋+∑i<j⌊xpipj⌋−∑i<j<k⌊xpipjpk⌋+⋯{displaystyle lfloor xrfloor -sum _{i}leftlfloor {frac {x}{p_{i}}}rightrfloor +sum _{i<j}leftlfloor {frac {x}{p_{i}p_{j}}}rightrfloor -sum _{i<j<k}leftlfloor {frac {x}{p_{i}p_{j}p_{k}}}rightrfloor +cdots }

(where ⌊x⌋{displaystyle lfloor {x}rfloor } denotes the floor function). This number is therefore equal to

π(x)−π(x)+1{displaystyle pi (x)-pi left({sqrt {x}}right)+1}

when the numbers p1,p2,…,pn{displaystyle p_{1},p_{2},ldots ,p_{n}} are the prime numbers less than or equal to the square root of x{displaystyle x}.

The Meissel–Lehmer algorithm

In a series of articles published between 1870 and 1885, Ernst Meissel described (and used) a practical combinatorial way of evaluating π(x){displaystyle pi (x)}. Let p1{displaystyle p_{1}}, p2,…,pn{displaystyle p_{2},ldots ,p_{n}} be the first n{displaystyle n} primes and denote by Φ(m,n){displaystyle Phi (m,n)} the number of natural numbers not greater than m{displaystyle m} which are divisible by no pi{displaystyle p_{i}}. Then

Φ(m,n)=Φ(m,n−1)−Φ(mpn,n−1).{displaystyle Phi (m,n)=Phi (m,n-1)-Phi left({frac {m}{p_{n}}},n-1right).}

Given a natural number m{displaystyle m}, if n=π(m3){displaystyle n=pi left({sqrt[{3}]{m}}right)} and if μ=π(m)−n{displaystyle mu =pi left({sqrt {m}}right)-n}, then

π(m)=Φ(m,n)+n(μ+1)+μ2−μ2−1−∑k=1μπ(mpn+k).{displaystyle pi (m)=Phi (m,n)+n(mu +1)+{frac {mu ^{2}-mu }{2}}-1-sum _{k=1}^{mu }pi left({frac {m}{p_{n+k}}}right).}

Using this approach, Meissel computed π(x){displaystyle pi (x)}, for x{displaystyle x} equal to 5×10⁵, 10⁶, 10⁷, and 10⁸.

In 1959, Derrick Henry Lehmer extended and simplified Meissel's method. Define, for real m{displaystyle m} and for natural numbers n{displaystyle n} and k{displaystyle k}, Pk(m,n){displaystyle P_{k}(m,n)} as the number of numbers not greater than m with exactly k prime factors, all greater than pn{displaystyle p_{n}}. Furthermore, set P0(m,n)=1{displaystyle P_{0}(m,n)=1}. Then

Φ(m,n)=∑k=0+∞Pk(m,n){displaystyle Phi (m,n)=sum _{k=0}^{+infty }P_{k}(m,n)}

where the sum actually has only finitely many nonzero terms. Let y{displaystyle y} denote an integer such that m3≤y≤m{displaystyle {sqrt[{3}]{m}}leq yleq {sqrt {m}}}, and set n=π(y){displaystyle n=pi (y)}. Then P1(m,n)=π(m)−n{displaystyle P_{1}(m,n)=pi (m)-n} and Pk(m,n)=0{displaystyle P_{k}(m,n)=0} when k{displaystyle k} ≥ 3. Therefore,

π(m)=Φ(m,n)+n−1−P2(m,n){displaystyle pi (m)=Phi (m,n)+n-1-P_{2}(m,n)}

The computation of P2(m,n){displaystyle P_{2}(m,n)} can be obtained this way:

P2(m,n)=∑y<p≤m(π(mp)−π(p)+1){displaystyle P_{2}(m,n)=sum _{y<pleq {sqrt {m}}}left(pi left({frac {m}{p}}right)-pi (p)+1right)},

where the sum is over prime numbers.

On the other hand, the computation of Φ(m,n){displaystyle Phi (m,n)} can be done using the following rules:

1. Φ(m,0)=⌊m⌋{displaystyle Phi (m,0)=lfloor mrfloor }


2. Φ(m,b)=Φ(m,b−1)−Φ(mpb,b−1){displaystyle Phi (m,b)=Phi (m,b-1)-Phi left({frac {m}{p_{b}}},b-1right)}

Using his method and an IBM 701, Lehmer was able to compute π(1010){displaystyle pi left(10^{10}right)}.

Further improvements to this method were made by Lagarias, Miller, Odlyzko, Deléglise and Rivat.^[13]

Other prime-counting functions

Other prime-counting functions are also used because they are more convenient to work with. One is Riemann's prime-counting function, usually denoted as Π0(x){displaystyle Pi _{0}(x)} or J0(x){displaystyle J_{0}(x)}. This has jumps of 1/n for prime powers pⁿ, with it taking a value halfway between the two sides at discontinuities. That added detail is used because then the function may be defined by an inverse Mellin transform. Formally, we may define Π0(x){displaystyle Pi _{0}(x)} by

Π0(x)=12(∑pn<x1n +∑pn≤x1n){displaystyle Pi _{0}(x)={frac {1}{2}}{bigg (}sum _{p^{n}<x}{frac {1}{n}} +sum _{p^{n}leq x}{frac {1}{n}}{bigg )}}

where p is a prime.

We may also write

Π0(x)=∑2xΛ(n)ln⁡n−12Λ(x)ln⁡x=∑n=1∞1nπ0(x1/n){displaystyle Pi _{0}(x)=sum _{2}^{x}{frac {Lambda (n)}{ln n}}-{frac {1}{2}}{frac {Lambda (x)}{ln x}}=sum _{n=1}^{infty }{frac {1}{n}}pi _{0}(x^{1/n})}

where Λ(n) is the von Mangoldt function and

π0(x)=limε→0π(x−ε)+π(x+ε)2.{displaystyle pi _{0}(x)=lim _{varepsilon rightarrow 0}{frac {pi (x-varepsilon )+pi (x+varepsilon )}{2}}.}

The Möbius inversion formula then gives

π0(x)=∑n=1∞μ(n)nΠ0(x1/n){displaystyle pi _{0}(x)=sum _{n=1}^{infty }{frac {mu (n)}{n}}Pi _{0}(x^{1/n})}

Knowing the relationship between log of the Riemann zeta function and the von Mangoldt function Λ{displaystyle Lambda }, and using the Perron formula we have

ln⁡ζ(s)=s∫0∞Π0(x)x−s−1dx{displaystyle ln zeta (s)=sint _{0}^{infty }Pi _{0}(x)x^{-s-1},dx}

The Chebyshev function weights primes or prime powers pⁿ by ln(p):

θ(x)=∑p≤xln⁡p{displaystyle theta (x)=sum _{pleq x}ln p}

ψ(x)=∑pn≤xln⁡p=∑n=1∞θ(x1/n)=∑n≤xΛ(n).{displaystyle psi (x)=sum _{p^{n}leq x}ln p=sum _{n=1}^{infty }theta (x^{1/n})=sum _{nleq x}Lambda (n).}

Formulas for prime-counting functions

Formulas for prime-counting functions come in two kinds: arithmetic formulas and analytic formulas. Analytic formulas for prime-counting were the first used to prove the prime number theorem. They stem from the work of Riemann and von Mangoldt, and are generally known as explicit formulas.^[14]

We have the following expression for ψ:

ψ0(x)=x−∑ρxρρ−ln⁡2π−12ln⁡(1−x−2),{displaystyle psi _{0}(x)=x-sum _{rho }{frac {x^{rho }}{rho }}-ln 2pi -{frac {1}{2}}ln(1-x^{-2}),}

where

ψ0(x)=limε→0ψ(x−ε)+ψ(x+ε)2.{displaystyle psi _{0}(x)=lim _{varepsilon rightarrow 0}{frac {psi (x-varepsilon )+psi (x+varepsilon )}{2}}.}

Here ρ are the zeros of the Riemann zeta function in the critical strip, where the real part of ρ is between zero and one. The formula is valid for values of x greater than one, which is the region of interest. The sum over the roots is conditionally convergent, and should be taken in order of increasing absolute value of the imaginary part. Note that the same sum over the trivial roots gives the last subtrahend in the formula.

For Π0(x){displaystyle Pi _{0}(x)} we have a more complicated formula

Π0(x)=li⁡(x)−∑ρli⁡(xρ)−ln⁡2+∫x∞dtt(t2−1)ln⁡t.{displaystyle Pi _{0}(x)=operatorname {li} (x)-sum _{rho }operatorname {li} (x^{rho })-ln 2+int _{x}^{infty }{frac {dt}{t(t^{2}-1)ln t}}.}

Riemann's explicit formula using the first 200 non-trivial zeros of the zeta function

Again, the formula is valid for x > 1, while ρ are the nontrivial zeros of the zeta function ordered according to their absolute value, and, again, the latter integral, taken with minus sign, is just the same sum, but over the trivial zeros. The first term li(x) is the usual logarithmic integral function; the expression li(x^ρ) in the second term should be considered as Ei(ρ ln x), where Ei is the analytic continuation of the exponential integral function from negative reals to the complex plane with branch cut along the positive reals.

Thus, Möbius inversion formula gives us^[15]

π0(x)=R⁡(x)−∑ρR⁡(xρ)−1ln⁡x+1πarctan⁡πln⁡x{displaystyle pi _{0}(x)=operatorname {R} (x)-sum _{rho }operatorname {R} (x^{rho })-{frac {1}{ln x}}+{frac {1}{pi }}arctan {frac {pi }{ln x}}}

valid for x > 1, where

R⁡(x)=∑n=1∞μ(n)nli⁡(x1/n)=1+∑k=1∞(ln⁡x)kk!kζ(k+1){displaystyle operatorname {R} (x)=sum _{n=1}^{infty }{frac {mu (n)}{n}}operatorname {li} (x^{1/n})=1+sum _{k=1}^{infty }{frac {(ln x)^{k}}{k!kzeta (k+1)}}}

is the so-called Riemann's R-function^[16] and μ(n) is the Möbius function. The latter series for it is known as Gram series^[17] and converges for all positive x.

Δ-function (red line) on log scale

The sum over non-trivial zeta zeros in the formula for π0(x){displaystyle pi _{0}(x)} describes the fluctuations of π0(x),{displaystyle pi _{0}(x),} while the remaining terms give the "smooth" part of prime-counting function,^[18] so one can use

R⁡(x)−1ln⁡x+1πarctan⁡πln⁡x{displaystyle operatorname {R} (x)-{frac {1}{ln x}}+{frac {1}{pi }}arctan {frac {pi }{ln x}}}

as the best estimator of π(x){displaystyle pi (x)} for x > 1.

The amplitude of the "noisy" part is heuristically about x/ln⁡x,{displaystyle {sqrt {x}}/ln x,} so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:

Δ(x)=(π0(x)−R⁡(x)+1ln⁡x−1πarctan⁡πln⁡x)ln⁡xx.{displaystyle Delta (x)=left(pi _{0}(x)-operatorname {R} (x)+{frac {1}{ln x}}-{frac {1}{pi }}arctan {frac {pi }{ln x}}right){frac {ln x}{sqrt {x}}}.}

An extensive table of the values of Δ(x) is available.^[7]

Inequalities

Here are some useful inequalities for π(x).

xln⁡x<π(x)<1.25506xln⁡x{displaystyle {frac {x}{ln x}}<pi (x)<1.25506{frac {x}{ln x}}}

for x ≥ 17.

The left inequality holds for x ≥ 17 and the right inequality holds for x > 1. The constant 1.25506 is 30ln⁡113113{displaystyle {frac {30ln 113}{113}}} to 5 decimal places, as π(x)ln⁡xx{displaystyle {frac {pi (x)ln x}{x}}} has its maximum value at x = 113.^[19]

Pierre Dusart proved in 2010:

xln⁡x−1<π(x){displaystyle {frac {x}{ln x-1}}<pi (x)} for x≥5393{displaystyle xgeq 5393}, and

π(x)<xln⁡x−1.1{displaystyle pi (x)<{frac {x}{ln x-1.1}}} for x≥60184{displaystyle xgeq 60184}.^[20]

Here are some inequalities for the nth prime, p_n. The upper bound is due to Rosser (1941),^[21] the lower one to Dusart (1999):^[22]

n(ln⁡(nln⁡n)−1)<pn<nln⁡(nln⁡n){displaystyle n(ln(nln n)-1)<p_{n}<n{ln(nln n)}!} for n ≥ 6.

The left inequality holds for n ≥ 2 and the right inequality holds for n ≥ 6.

An approximation for the nth prime number is

pn=n(ln⁡(nln⁡n)−1)+n(ln⁡ln⁡n−2)ln⁡n+O(n(ln⁡ln⁡n)2(ln⁡n)2).{displaystyle p_{n}=n(ln(nln n)-1)+{frac {n(ln ln n-2)}{ln n}}+Oleft({frac {n(ln ln n)^{2}}{(ln n)^{2}}}right).}

In his well-known notebooks, Ramanujan^[23] proves that the inequality

π(x)2<exlog⁡xπ(xe){displaystyle pi (x)^{2}<{frac {ex}{log x}}pi {bigg (}{frac {x}{e}}{bigg )}}

holds for all sufficiently large values of x{displaystyle x}.

The Riemann hypothesis

The Riemann hypothesis is equivalent to a much tighter bound on the error in the estimate for π(x){displaystyle pi (x)}, and hence to a more regular distribution of prime numbers,

π(x)=li⁡(x)+O(xlog⁡x).{displaystyle pi (x)=operatorname {li} (x)+O({sqrt {x}}log {x}).}

Specifically,^[24]

|π(x)−li⁡(x)|<18πxlog⁡x,for all x≥2657.{displaystyle |pi (x)-operatorname {li} (x)|<{frac {1}{8pi }}{sqrt {x}},log {x},qquad {text{for all }}xgeq 2657.}

See also

• Foias constant


• Bertrand's postulate


• Oppermann's conjecture


• Ramanujan prime

References

External links

• Chris Caldwell, The Nth Prime Page at The Prime Pages.


• Tomás Oliveira e Silva, Tables of prime-counting functions.