Rearuh

在這篇文章內，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 r{displaystyle mathbf {r} ,!} 表示；而其大小則用 r{displaystyle r,!} 來表示。

一個平面波的波前行進於空間。

在三維空間裏，平面波（plane wave）是一種波動，其波阵面（在任何時刻，波相位相等的每一點所形成的曲面）是相互平行的平面。平面波的傳播方向垂直於波前。假若平面波的振幅不是常數，例如，振幅是位置的函數，則稱此種平面波為「非均勻平面波」。^[1]:24-27

加以延伸，平面波這術語時常用來形容，在空間的一個局部區域裏，近似於平面波的波動。例如，一個局部區域波源，像發射無線電波的天線，所發射出的電磁波，在遠場區（英语：far-field region）可以近似為平面波。等價地說，對於在一個均勻介質內，波的傳播距離超長於波長的案例，在幾何光學的正確極限內，射線區域性地對應於近似平面波。

數學表述

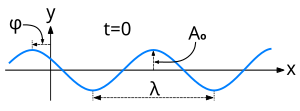
在时间等于零时，正相移导致波向左移位。

随着t增加，波向右移动，给定点x处的值振荡正弦波。

3D平面波的动画。 每种颜色表示波的不同的相位。

用數學來表述，波動方程式為

∇2f−1v2∂2f∂t2=0{displaystyle nabla ^{2}f-{frac {1}{v^{2}}}{frac {partial ^{2}f}{partial t^{2}}}=0} ；

其中，f(x,t){displaystyle f(mathbf {x} ,t)} 是描述波動的函數，∇2{displaystyle nabla ^{2}} 是拉普拉斯算符，v{displaystyle v} 是波動傳播的速度，x{displaystyle mathbf {x} } 是位置，t{displaystyle t} 是時間。

描述平面波的函數 ψ~(x,t){displaystyle {tilde {psi }}(mathbf {x} ,t)} 是波動方程式的一種解答：

∇2ψ~−1v2∂2ψ~∂t2=0{displaystyle nabla ^{2}{tilde {psi }}-{frac {1}{v^{2}}}{frac {partial ^{2}{tilde {psi }}}{partial t^{2}}}=0} 。

平面波 ψ~(x,t){displaystyle {tilde {psi }}(mathbf {x} ,t)} 的形式為：

ψ~(x,t)=A~ei(k⋅x−ωt){displaystyle {tilde {psi }}(mathbf {x} ,t)={tilde {A}}e^{i(mathbf {k} cdot mathbf {x} -omega t)}} ；

其中，i{displaystyle i} 是虛數單位，k{displaystyle mathbf {k} } 是波向量，ω=kv{displaystyle omega =kv} 是角頻率，A~{displaystyle {tilde {A}}} 是複值的振幅純量。

取複函數的實部，則可以得到其物理意義。

Re⁡{ψ~(x,t)}=|A~|cos⁡(k⋅x−ωt+arg⁡A~){displaystyle operatorname {Re} {{tilde {psi }}(mathbf {x} ,t)}=|{tilde {A}}|cos(mathbf {k} cdot mathbf {x} -omega t+arg {tilde {A}})} 。

注意到在任意時刻 t=t0{displaystyle t=t_{0}} ，波相位不變的曲面滿足方程式

k⋅x−ωt0+arg⁡A~=c1{displaystyle mathbf {k} cdot mathbf {x} -omega t_{0}+arg {tilde {A}}=c_{1}} ，

或者，

k⋅x=c2{displaystyle mathbf {k} cdot mathbf {x} =c_{2}} ；

其中，c1{displaystyle c_{1}} 、c2{displaystyle c_{2}} 是任意常數。

所有滿足這方程式的 x{displaystyle mathbf {x} } 形成一個與 k{displaystyle mathbf {k} } 相互垂直的平面，平行波的波前就是這種平面，所有的波前都與 k{displaystyle mathbf {k} } 相互垂直，都相互平行。

對於向量的波動方程式，像描述在彈性固體內的機械波或電磁波的波動方程式：

∇2E−1v2∂2E∂t2=0{displaystyle nabla ^{2}mathbf {E} -{frac {1}{v^{2}}}{frac {partial ^{2}mathbf {E} }{partial t^{2}}}=0} ，

∇2B−1v2∂2B∂t2=0{displaystyle nabla ^{2}mathbf {B} -{frac {1}{v^{2}}}{frac {partial ^{2}mathbf {B} }{partial t^{2}}}=0} ；

其中，E{displaystyle mathbf {E} } 是電場，B{displaystyle mathbf {B} } 是磁場;

解答也很類似：

ψ~(x, t)=A~ei(k⋅x−ωt){displaystyle {tilde {boldsymbol {psi }}}(mathbf {x} , t)={tilde {mathbf {A} }}e^{i(mathbf {k} cdot mathbf {x} -omega t)}} ；

其中，A~{displaystyle {tilde {mathbf {A} }}} 是複值的振幅向量。

横波的振幅向量垂直於波向量，像傳播於均向性介質的電磁波。縱波的振幅向量平行於波向量，像傳播於氣體或液體的聲波。

傳播於某介質內，角頻率與波向量之間的關係，可以以函數 ω(k){displaystyle omega (mathbf {k} )} 表達，稱為介質的色散關係。對於這介質，波的相速度是

vp=ω/k{displaystyle v_{p}=omega /k} ，

群速度是

vg=∂ω∂k{displaystyle v_{g}={frac {partial omega }{partial mathbf {k} }}} 。

参阅

• 波动方程

參考文獻