Decagram (geometry)
| Regular decagram | |
|---|---|
 A regular decagram | |
| Type | Regular star polygon |
Edges and vertices | 10 |
| Schläfli symbol | {10/3} t{5/3} |
| Coxeter diagram | |
| Symmetry group | Dihedral (D10) |
Internal angle (degrees) | 72° |
| Dual polygon | self |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
| Star polygons |
|---|
|
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is {10/3}.[1]
The name decagram combine a numeral prefix, deca-, with the Greek suffix -gram. The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[2]
Contents
1 Regular decagram
2 Applications
3 Related figures
4 See also
5 References
Regular decagram
For a regular decagram with unit edge lengths, the proportions of the crossing points on each edge are as shown below.

Applications
Decagrams have been used as one of the decorative motifs in girih tiles.[3]
Related figures
A regular decagram is a 10-sided polygram, represented by symbol {10/n}, containing the same vertices as regular decagon. Only one of these polygrams, {10/3} (connecting every third point), forms a regular star polygon, but there are also three ten-vertex polygrams which can be interpreted as regular compounds:
- {10/5} is a compound of five degenerate digons 5{2}
- {10/4} is a compound of two pentagrams 2{5/2}
- {10/2} is a compound of two pentagons 2{5}.[4][5]
| Form | Convex | Compound | Star polygon | Compounds | |
|---|---|---|---|---|---|
| Image |  |  |  |  |  |
| Symbol | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
{10/2} can be seen as the 2D equivalent of the 3D compound of dodecahedron and icosahedron and 4D compound of 120-cell and 600-cell; that is, the compound of two pentagonal polytopes in their respective dual positions.
{10/4} can be seen as the two-dimensional equivalent of the three-dimensional compound of small stellated dodecahedron and great dodecahedron or compound of great icosahedron and great stellated dodecahedron through similar reasons. It has six four-dimensional analogues.
Deeper truncations of the regular pentagon and pentagram can produce intermediate star polygon forms with ten equally spaced vertices and two edge lengths that remain vertex-transitive (any two vertices can be transformed into each other by a symmetry of the figure).[6][7][8]
| Quasiregular | Isogonal | Quasiregular Double covering | |
|---|---|---|---|
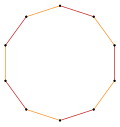 t{5} = {10} | 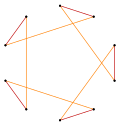 |  |  t{5/4} = {10/4} = 2{5/2} |
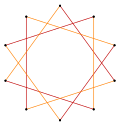 t{5/3} = {10/3} |  | 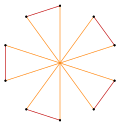 |  t{5/2} = {10/2} = 2{5} |
See also
- List of regular polytopes and compounds#Stars
References
| Wikimedia Commons has media related to Ten pointed stars. |
^ Barnes, John (2012), Gems of Geometry, Springer, pp. 28–29, ISBN 9783642309649.mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}.
^ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
^ Sarhangi, Reza (2012), "Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons", Bridges 2012: Mathematics, Music, Art, Architecture, Culture (PDF), pp. 165–174.
^ Regular polytopes, p 93-95, regular star polygons, regular star compounds
^ Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38
^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum.
^ *Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 411. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.
^ Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consists of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.