Pentagrammic antiprism
Uniform Pentagrammic antiprism | |
|---|---|
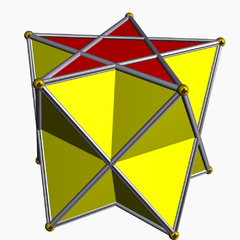 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 12, E = 20 V = 10 (χ = 2) |
| Faces by sides | 10{3}+2{5/2} |
| Schläfli symbol | sr{2,5/2} |
| Wythoff symbol | | 2 2 5/2 |
| Coxeter diagram | |
| Symmetry | D5h, [5,2], (*552), order 20 |
| Rotation group | D5, [5,2]+, (55), order 10 |
| Index references | U79(a) |
| Dual | Pentagrammic trapezohedron |
| Properties | nonconvex |
 Vertex figure 3.3.3.5/2 | |
In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
This polyhedron is identified with the indexed name U79 as a uniform polyhedron.

An alternative representation with hollow centers to the pentagrams.
Net
Net (fold the dotted line in the centre in the opposite direction to all the other lines):

See also
- Prismatic uniform polyhedron
- Pentagrammic prism
- Pentagrammic crossed-antiprism
External links
- Weisstein, Eric W. "Pentagrammic antiprism". MathWorld..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
- http://www.mathconsult.ch/showroom/unipoly/04.html
- https://web.archive.org/web/20050313233653/http://www.math.technion.ac.il/~rl/kaleido/data/04.html
This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |