Golden triangle (mathematics)

A golden triangle. The ratio a:b is equivalent to the golden ratio φ.

Golden gnomon.
A golden triangle, also known as the sublime triangle,[1]is an isosceles triangle in which the duplicated side is in the golden ratio to the distinct side:
- ab=φ=1+52.{displaystyle {a over b}=varphi ={1+{sqrt {5}} over 2}.}
Golden triangles are found in the nets of several stellations of dodecahedrons and icosahedrons.
Also, it is the shape of the triangles found in the points of pentagrams.
The vertex angle is equal to
- θ=cos−1(φ2)=π5=36∘.{displaystyle theta =cos ^{-1}left({varphi over 2}right)={pi over 5}=36^{circ }.}
Since the angles of a triangle sum to 180°, base angles are therefore 72° each.[1]
The golden triangle can also be found in a regular decagon, or an equiangular and equilateral ten-sided polygon, by connecting any two adjacent vertices to the center. This will form a golden triangle. This is because:
180(10-2)/10=144 degrees is the interior angle and bisecting it through the vertex to the center, 144/2=72.[1]
The golden triangle is also uniquely identified as the only triangle to have its three angles in 2:2:1 proportions.[2]
Contents
1 Logarithmic spiral
2 Golden gnomon
3 See also
4 References
5 External links
Logarithmic spiral

Golden triangles inscribed in a logarithmic spiral
The golden triangle is used to form a logarithmic spiral. By bisecting the base angles, a new point is created that in turn, makes another golden triangle.[3]
The bisection process can be continued infinitely, creating an infinite number of golden triangles. A logarithmic spiral can be drawn through the vertices. This spiral is also known as an equiangular spiral, a term coined by René Descartes. "If a straight line is drawn from the pole to any point on the curve, it cuts the curve at precisely the same angle," hence equiangular.[4]
Golden gnomon
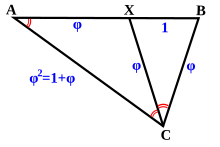
Golden triangle bisected in Robinson triangles: a golden triangle and a golden gnomon.

A pentagram. Each corner is a golden triangle. The figure also contains five golden gnomons, made by joining two corners that are not adjacent to the central pentagon.
Closely related to the golden triangle is the golden gnomon, which is the obtuse isosceles triangle in which the ratio of the length of the equal (shorter) sides to the length of the third side is the reciprocal of the golden ratio. The golden gnomon is also uniquely identified as a triangle having its three angles in 1:1:3 proportion. The acute angle is 36 degrees, which is the same as the apex of the golden triangle.
The distance of AX and CX are both equal to φ, as seen in the figure. "The golden triangle has a ratio of base length to side length equal to the golden section φ, whereas the golden gnomon has the ratio of side length to base length equal to the golden section φ."[5]
A golden triangle can be bisected into a golden triangle and a golden gnomon. The same is true for a golden gnomon. A golden gnomon and a golden triangle with their equal sides matching each other in length, are also referred to as the obtuse and acute Robinson triangles.[2]
These isosceles triangles can be used to produce Penrose tilings. Penrose tiles are made from kites and darts. A kite is made from two golden triangles, and a dart is made from two gnomons.
See also
- Golden rectangle
- Golden rhombus
- Kepler triangle
- Kimberling's golden triangle
- Lute of Pythagoras
- Pentagram
References
^ abc
Elam, Kimberly (2001). Geometry of Design. New York: Princeton Architectural Press. ISBN 1-56898-249-6..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ ab
Tilings Encyclopedia. 1970. Archived from the original on 2009-05-24.
^
Huntley, H.E. (1970). The Divine Proportion: A Study In Mathematical Beauty. New York: Dover Publications Inc. ISBN 0-486-22254-3.
^
Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
^
Loeb, Arthur (1992). Concepts and Images: Visual Mathematics. Boston: Birkhäuser Boston. p. 180. ISBN 0-8176-3620-X.
External links
- Weisstein, Eric W. "Golden triangle". MathWorld.
- Weisstein, Eric W. "Golden gnomon". MathWorld.
Robinson triangles at Tilings Encyclopedia- Golden triangle according to Euclid
The extraordinary reciprocity of golden triangles at Tartapelago by Giorgio Pietrocola


