紅移

上圖右側為遙遠的星系在可見光波段的光譜,與圖左側太陽的光譜比較,可以看見譜線朝紅色的方向移動,即波長增加(頻率降低)
在物理學领域,紅移(Redshift)是指電磁輻射由於某种原因導致波长增加、頻率降低的现象,在可見光波段,表现为光谱的谱线朝紅端移動了一段距离。相反的,電磁輻射的波長变短、频率升高的现象则被稱為藍移。紅移最初是在人们熟悉的可见光波段发现的,随着对电磁波谱各个波段的了解逐步加深,任何电磁辐射的波長增加都可以称为紅移。对於波长较短的γ射線、X-射線和紫外線等波段,波长变长确实是波谱向红光移动,“红移”的命名并无问题;而对於波长较长的紅外線、微波和無線電波等波段,尽管波长增加實際上是遠離红光波段,这种现象还是被称为“红移”。
當光源移動遠離觀測者时,观测者观察到的电磁波谱會發生紅移,这类似于聲波因为都卜勒效應造成的頻率變化。這樣的紅移现象在日常生活中有很多應用,例如都卜勒雷達、雷達槍[1][2],在天體光譜學裏,人们使用都卜勒紅移測量天體的物理行為[3][4][5]。
另一種紅移稱為宇宙學紅移,其機制為空間的度規膨脹。這機制說明了在遙遠的星系、類星體,星系間的氣體雲的光谱中觀察到的红移现象,其紅移增加的比例與距離成正比。這種關係为宇宙膨脹的观点提供了有力的支持,比如大霹靂宇宙模型[6][7]。
另一種形式的紅移是引力紅移,其為一種相對論性效應,當電磁輻射傳播遠離引力場時會觀測到這種效應;反過來說,當電磁輻射傳播接近引力場時會觀測到引力藍移,其波長變短、频率升高[6][7]。
红移的大小由“红移值”衡量,红移值用Z表示,定义为:
- z=λ−λ0λ0=f0−ff{displaystyle z={frac {lambda -lambda _{0}}{lambda _{0}}}={frac {f_{0}-f}{f}}}
这裡λ0{displaystyle lambda _{0},}



目录
1 分類
2 簡史
3 測量、特性和解釋
4 機制
4.1 都卜勒效應
4.2 相對論性都卜勒效應
4.3 膨脹的宇宙
4.4 重力紅移
5 天文學的觀測
5.1 在本地群的觀測
5.2 外星系的觀察
5.3 紅移巡天
6 來自物理的光學或輻射轉換的效應
7 注释
8 參考資料
9 延伸阅读
10 外部連結
11 相關條目
分類
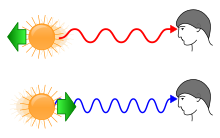
光源相对观测者的运动导致红移和蓝移
多普勒紅移:物体和观察者之间的相对运动可以导致红移,与此相对应的红移称为多普勒红移,是由多普勒效应引起的。
重力紅移:根据广义相对论,光从重力場中发射出来时也会发生红移的现象。这种红移称为重力紅移。
宇宙學紅移:20世纪初,美国天文学家愛德文·哈勃发现,观测到的绝大多数星系的光谱线存在红移现象。这是由於宇宙空间在膨胀,使天体發出的光波被拉長,谱线因此“变红”,这稱為宇宙學紅移,并由此得到哈伯定律。20世纪60年代发现了一类具有极高红移值的天体:类星体,成为近代天文学中非常活跃的研究领域。
簡史
這個主題的發展開始於19世紀對波動力學現象的探索,因而連結到了都卜勒效應。稍後,因為克里斯琴·多普勒在1842年對這種現象提出了物理學上的解釋,而被稱為都卜勒效應[8]。他的假說在1845年被荷蘭的科學家赫里斯托福鲁斯·亨里克斯·迪德里克斯·白贝罗用聲波做實驗而獲得證實[9]。都卜勒預言這種現象可以應用在所有的波上,並且指出恆星的顏色不同可能是由于它们相对于地球的运动速度不同而引起的[10]。后来這個推論被否认。恆星呈現不同的顏色是因為溫度不同,而不是運動速度不同。
都卜勒紅移是法國物理學家阿曼德·斐索在1848年首先發現的,他指出恆星譜線位置的移動是由于都卜勒效應,因此也稱為“都卜勒-斐索效應”。1868年,英國天文學家威廉·哈金斯首次測出了恆星相对于地球的运动速度[11]。
在1871年,利用太陽的自轉測出在可見光太陽光譜的夫朗和斐譜線在紅光有0.1 Å的位移。[12]在1901年,亞里斯塔克·貝樓坡斯基在實驗室中利用轉動的鏡片證明了可見光的紅移[13]。
在1912年開始的觀測,維斯托·斯里弗發現絕大多數的螺旋星雲都有不可忽視的紅移。[a]然後,埃德温·哈伯發現這些星雲(現在知道是星系)的紅移和距離有關聯性,也就是哈伯定律。[16]這些觀察在今天被認為是造成宇宙膨脹大爆炸理论的強而有力證據。[b]
測量、特性和解釋
紅移可以經由單一光源的光譜進行測量(參考上面理想化的光譜例証圖)。如果在光譜中有一些特徵,可以是吸收線、發射線、或是其他在光強上的變化,那麼原則上紅移就可以測量。這需要一個有相似特徵的光譜來做比較,例如當氫原子發出光線時,其光谱有明確的特徵譜線,而这一系列的特色譜線都有一定間隔的。如果有這種特性的譜線型態但在不同的波長上被比對出來,那麼這個物體的紅移就能測量了。因此,測量一個物體的紅移,只需要頻率或是波長的範圍。只觀察到一些孤立的特徵,或是沒有特徵的光譜,或是白噪音(一種相當無序雜亂的波),是無法計算紅移的。[c]
紅移(和藍移)可能會在天體被觀測的和輻射的波長(或頻率)而帶有不同的變化特徵,天文學習慣使用无量纲的數量z來表示。如果λ代表波長,f代表頻率(注意:λf = c,此處的c是光速),那麼z可以由下面的公式來定義:
| 以波長為基礎 | 以頻率為基礎 |
|---|---|
z=λo−λeλe{displaystyle z={frac {lambda _{mathrm {o} }-lambda _{mathrm {e} }}{lambda _{mathrm {e} }}}}  | z=fe−fofo{displaystyle z={frac {f_{mathrm {e} }-f_{mathrm {o} }}{f_{mathrm {o} }}}}  |
1+z=λoλe{displaystyle 1+z={frac {lambda _{mathrm {o} }}{lambda _{mathrm {e} }}}}  | 1+z=fefo{displaystyle 1+z={frac {f_{mathrm {e} }}{f_{mathrm {o} }}}}  |
| 下標e和o分別表示發出的和觀察到的量 | |
在z被測量後,紅移和藍移的差別只是簡單的正負號的區別。依據下一章節的機制,無論被觀察到的是紅移或藍移,都有一些基本的說明。例如,都卜勒效應的藍移(z < 0)會聯想到物體朝向觀測者接近並且能量增加,反過來說都卜勒紅移(z > 0),就會聯想到物體遠離觀測者而去並且能量減少。同樣的,愛因斯坦效應的藍移可以聯想到光線進入強引力場,而愛因斯坦效應的紅移是離開引力場。
機制
一個光子在真空中傳播可以有幾種不同的紅移機制,每一種機制都能產生類似都卜勒紅移的現象,意謂著z是與波長無關的。這些機制分別使用伽利略变换、勞侖茲變換、或相對論轉換在各個參考架構之間來比較。[3][4][5]
| 紅移型式 | 轉換的架構 | 所在度規 | 定義[d] |
|---|---|---|---|
| 都卜勒紅移 | 伽利略轉換 | 欧几里得度规 | z=vc{displaystyle z={frac {v}{c}}}  |
| 相對論性都卜勒 | 勞侖茲變換 | 闵可夫斯基度规 | z=(1+vc)γ−1{displaystyle z=left(1+{frac {v}{c}}right)gamma -1}  |
| 宇宙論的紅移 | 廣義相對論轉換 | FRW度规 | z=anowathen−1{displaystyle z={frac {a_{mathrm {now} }}{a_{mathrm {then} }}}-1}  |
| 重力紅移 | 廣義相對論轉換 | 史瓦西度规 | z=11−(2GMrc2)−1{displaystyle z={frac {1}{sqrt {1-left({frac {2GM}{rc^{2}}}right)}}}-1}  |
都卜勒效應
如果一個光源是遠離觀測者而去,那麼會發生紅移(z > 0),當然,如果光源是朝向觀測者移動,便會產生藍移(z < 0)。這對所有的電磁波都適用,而且可以用都卜勒效應解釋。當然的結果是,這種形式的紅移被稱為都卜勒紅移。如果光源遠離觀測者的速度是v,忽略掉相對論的效應,紅移可以表示為:
z≈vc{displaystyle zapprox {frac {v}{c}}}(由于 γ≈1{displaystyle gamma approx 1}
, 參考下面的說明)
此處c是光速,在古典的都卜勒效應,光源的的頻率是無需修正的,但是退行會造成低頻的錯覺。
對于聲波等機械波,也有這樣的效應。当波源向觀察者運動時,觀察者接受到的波的頻率變高;波源離開時則反之。
相對論性都卜勒效應
更完整的都卜勒紅移需要考慮相對論的效應,特別是在速度接近光速的情況下。完整的文章可以參考相對論性都卜勒效應。簡單的說,物體的運動接近光速時需要將狹義相對論介紹的時間膨脹因素勞侖茲變換因子γ引入古典的都卜勒公式中,改正後的形式如下:
- 1+z=(1+vc)γ{displaystyle 1+z=left(1+{frac {v}{c}}right)gamma }
這種現象最早是在1938年赫伯特·艾凡斯和G. R. 史迪威進行的實驗中被觀察到的,稱為艾凡斯-史迪威實驗。[18]
由於羅倫茲因子只與速度的量值有關,這使得红移與相對論的相關只獨立的與來源的運動取向有關。在對照時,古典這一部分的形式只與來源的運動投影在視線方向上的分量有關,因此在不同的方向上會得到不同的結果。同樣的,一個運動方向與觀測者之間有θ的角度(正對著觀測者時角度為0),完整的相對論性都卜勒效應形式為:[19]
- 1+z=1−vcos(θ)/c1−v2/c2{displaystyle 1+z={frac {1-vcos(theta )/c}{sqrt {1-v^{2}/c^{2}}}}}
而正對著觀測者的運動物體(θ = 0°),公式可以簡化為:
- 1+z=1+vc1−vc{displaystyle 1+z={sqrt {frac {1+{frac {v}{c}}}{1-{frac {v}{c}}}}}}
在特殊的狀況下,運動源與測器成直角(θ = 90°),相對性的紅移為橫向紅移[20],儘管物體並沒有移動遠離觀測者,仍舊會測量到紅移
- 1+z=11−v2/c2{displaystyle 1+z={frac {1}{sqrt {1-v^{2}/c^{2}}}}}
即時來源是朝向觀測者運動,如果有橫向的分量,那麼在這個方向上的速度可以增加到抵消預期中的藍移,而且如果繼續增加速度,則會使朝向觀測者的來源呈現紅移。
膨脹的宇宙
在20世紀初期,史立佛、哈伯和其他人,首度測量到銀河系之外星系的紅移和藍移,他們起初很單純的解釋是都卜勒效應造成的紅移和藍移,但是稍後哈伯發現距離和紅移之間有著粗略的關聯性,距離越遠紅移的量也越大。理論學者幾乎立刻意識到這些觀察到的紅移可以用另一個不同的機制來解釋,哈伯定律就是紅移和距離之間交互作用的關聯性,需要使用廣義相對論空間的度規膨脹的宇宙論模型來解釋。[21]結果是,光子在通過擴張的空間時被延展,產生了宇宙學紅移。這與都卜勒效應所描述的因速度增加所產生的紅移不同(這是勞侖茲變換),在光源和觀測者之間不是因為動量和能量的轉換,取代的是光子因為經過膨脹的空間使波長增加而紅移。[22]這種效應在標準宇宙學模型中被解釋為可以觀測到與時間相關聯的宇宙標度因子(a{displaystyle a}
1+z=anowathen{displaystyle 1+z={frac {a_{mathrm {now} }}{a_{mathrm {then} }}}}。
這種型態的紅移稱為“宇宙學紅移”或“哈伯紅移”。如果宇宙是收縮而不是膨脹,我們將觀測到星系以相同比例的藍移取代紅移。[e]
這些星系不是以實際的速度遠離觀測者而去,取代的是在其間的空間延展,這造成了大尺度下宇宙論原則所需要的各向同性的現象。[24]在宇宙學紅移z < 0.1的情況下,時空擴展的作用對星系所造成的獨特效應與被觀察到的紅移,相對於都卜勒效應的紅移和藍移是極微小的。[f]
實際的速度和空間膨脹的之間的區別在膨脹的橡皮板宇宙有清楚的說明,一般的宇宙學也曾經描述過類似的空間擴展。如果以滾珠軸承來代表兩個物體,以有彈性的橡皮墊代表時空,都卜勒效應是軸承橫越過橡皮墊產生的獨特運動,宇宙學紅移則是橡皮墊向下沉陷的柱狀體的沉陷量。(很明顯的在模型上會有維度的問題,當軸承滾動時應該是在橡皮墊上,而如果兩個物體的距離夠遠時宇宙學紅移的速度會大於都卜勒效應的速度。)
儘管速度是由分別由都卜勒紅移和宇宙學紅移共同造成的,天文學家(特別是專業的)有時會以"退行速度"來取代在膨脹宇宙中遙遠的星系的紅移,即使很明顯的只是視覺上的退行[26]。影響所及,在大眾化的講述中經常會以"都卜勒紅移"而不是"宇宙學紅移"來描述受到時空擴張影響下的星系運動,而不會注意到在使用相對論的場合下計算的"宇宙學退行速度"不會與都卜勒效應的速度相同。
[27]明確的說,都卜勒紅移只適用於狹義相對論,因此v > c是不可能的;而相對的,在宇宙學紅移中v > c是可能的,因為空間會使物體(例如,從地球觀察類星體)遠離的速度超過光速。[g]更精確的,"遙遠的星系退行"的觀點和"空間在星系之間擴展"的觀點可以通過坐標系統的轉換來連繫。 要精確的表達必須要使用數學的罗伯逊-沃尔克度规。[28]
重力紅移

由中子星造成的引力紅移的圖解表示。
在廣義相對論的理論中,引力會造成時間的膨脹,這就是所謂的引力紅移或是愛因斯坦位移[29]。這個作用的理論推導從爱因斯坦场方程的施瓦氏解,以一顆光子在不帶電荷、不轉動、球對稱質量的重力場運動,產生的紅移:
1+z=11−(2GMrc2){displaystyle 1+z={frac {1}{sqrt {1-left({frac {2GM}{rc^{2}}}right)}}}},
其中G{displaystyle G}



引力紅移的結果可以從狹義相對論和等效原理導出,並不需要完整的廣義相對論[30]。
在地球上這種效應非常小,但是經由穆斯堡尔效應依然可以測量出來,並且在庞德-雷布卡实验中首次得到驗證[31]。然而,在黑洞附近就很顯著,當一個物體接近事件視界時,紅移將變成無限大,他也是在宇宙微波背景辐射中造成大角度尺度溫度擾動的主要角色[i][32]。
天文學的觀測
在天文觀測中可以測量到紅移,因為原子的發射光譜和吸收光譜,與在地球上的實驗室內的分光儀校準好的光譜比較時,是非常的明顯。當從同一個天體上測量到各種不同的吸收和發射譜線時,z被發現是一個常數。雖然來自遙遠天體的譜線可能會被污染,並且有輕微的變寬,但並不能夠用熱力學或機械的行為來解釋。基於這些和其他的理由,公眾的輿論已經將天文學上觀測到的紅移認定是三種類似的都卜勒紅移之一,而沒有任何一種假說能如此的振振有詞。[j]
光譜學,用在測量上,比只要簡單的通過特定的濾光器來測定天體亮度的光度學要困難。[35]當測光時,可以利用所有的數據(例如,哈勃深空和哈勃超深空),天文學家依靠的是紅移測光的技術,[36]由於濾光器在某些波長的範圍內非常靈敏,依靠這樣的技術可以假定許多光譜的本質隱藏在光源之內,觀測誤差可以δz = 0.5為級距來排序,並且比分光鏡的更為可靠許多。[37]然而,光度學無法考慮到紅移的定性描述。例如,一個與太陽相似的光譜,但紅移z = 1,最為明亮的是在紅外線的區域,而非以黃-綠為尖峰的黑體光譜,並且光的強度在經過濾光器時將減少二級(1+z,更多的細節請參考紅移測光的K校正。[k]
在本地群的觀測
在附近的目標(在我們的銀河系內的天體)觀測到的紅移幾乎都與相對於視線方向上的速度有關。觀察這樣的紅移和藍移,讓天文學家可以測量速度和分光雙星的參考質量。這種方法是英國天文學家威廉·哈金斯在1868年最先採用的。[11]相同的,從光譜儀中對單獨的一顆恆星所測得的微量的紅移和藍移是天文學家檢測是否有行星系環繞著恆星的診斷和測量的方法之一。[l]對紅移更精確的測量被應用於日震學上,藉以精確的測量太陽光球的運動。[40]紅移也被應用於第一次的行星自轉速率的測量[m]、星際雲的速度[41]、星系的自轉[3][4][5],還有吸積的動力學呈現在中子星和黑洞的都卜勒和重力紅移。[42]
另外,還有各種不同輻射和吸收的溫度造成的都卜勒增寬——對單一的吸收或輻射譜線造成的紅移和藍移的效應。[43]測量來自不同方向的氫線21公分波的擴展和轉移,天文學家能測量出星際氣體的退行速度,揭露出我們銀河系的自轉曲線。[3][4][5]相同的測量也被應用在其他的星系,例如仙女座星系。[3][4][5]做為一種診斷的工具,紅移測量在天文學的分光學中是最重要的工具之一。
外星系的觀察
宇宙中合於哈伯定律的天體距離越遠就有越大的紅移,因此被觀測到有最大紅移,對應於最遙遠的距離也有最長的回應時間的天體是宇宙微波背景辐射,紅移的數值高達z = 1089(z = 0相當於現在的時間),在宇宙年齡為137億年的狀態下,相當於大霹靂之後379,000年的時間。[n]
核心像點光源的類星體是紅移(z>0.1{displaystyle z>0.1}



對比本星系群遙遠,但仍在室女座星系團附近,距離為10億秒差距左右的星系,紅移與星系的距離是近似成比例的,這種關係最早是由哈伯發現的,也就是眾所皆知的哈伯定律。星系紅移最早是维斯托·斯莱弗大約在1912年發現的,而哈伯結合了斯莱弗的測量成為度量天體距離的另一種方法:哈伯定律。在建基於廣義相對論下被廣泛接受的宇宙模型中,紅移是空間擴展的主要結果:這意味著遙遠的星系都離我們而去,光離開星系越久,空間的擴展也越多,所以光也就被延伸越多,紅移的值也就越大,所以越遠的看起來就移動的越快。哈伯定律一樣適用哥白尼原則,由於我們通常不知道天體有多明亮,測量紅移會比直接測量距離容易,所以使用哈伯定律就可以得知天體大略的距離。
星系之間的和星系團的重力交互作用在正常的哈伯圖上導致值得注意的消散,星系的本動速度和在宇宙中的維理天體的迷蹤質量相疊加,這種作用導致在附近的星系(像仙女座星系)顯示出藍移的現象,並且向共同的重心接近,同時星系團的紅移圖像上帝的手指在作用使本動速度的消散大致成球型的分佈。[24]這個增加的組合給了宇宙學家一個單獨測量質量的“質光比”(以太陽的質量和光為單位的星系的質量與光度比值),是尋找暗物質的重要工具。[48]
對更遙遠的星系,目前的距離和紅移之間的關連性變得更為複雜。當你看見一個遙遠的星系,也就是看見相同久遠之前的星系,而那時的宇宙和現在是不同的。在那些早期的時刻,我們期待在俇展的速率上有所不同,原因至少有二個:
- 星系之間相互的重力吸引會減緩宇宙的擴張行動
- 可能存在的宇宙學常數或第五元素與可能會改變宇宙擴張的速率。
[49]
最近的觀測卻建議宇宙的擴張不僅沒有如同第一點的預測減速,反而在加速中。[50][51]這是廣泛的,雖然不是相當普遍的,相信這是因為有暗物質在控制著宇宙的發展。這樣的宇宙學常數暗示宇宙的最後命運不是大擠壓,反而可預見宇宙將長久存在。(可是在宇宙內多數的物理程序仍然朝向熱寂。)
擴張的宇宙是大霹靂理論的中心預言,如果往前追溯,理論預測“奇點”的存在,而那時的宇宙有無限大的密度;廣義相對論的理論,大霹靂的理論依據,將不再能適用。[24]:77最有可能取代的理論據信是尚未成熟的量子引力學,能在密度變得無窮大之前繼續適用。[6]:§28.3[7]:595-596
紅移巡天
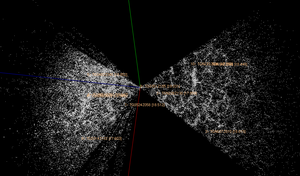
2度視場星系紅移巡天資料最精華的資料
在先進的自動化望遠鏡和改良的光譜儀合作之下,以一定數量星空的紅移當成宇宙的投影,通過紅移與角度位置數據的結合,紅移巡天圖可以顯示天空中一定範圍內物質的立體分布狀態。這些觀測被用來研究宇宙的大尺度結構,長城、許多廣達5億光年的超星系團,紅移巡天的檢測提供了戲劇性的大尺度構造的例子。
[52]
第一次紅移巡天是CfA紅移巡天,開始於1977年,至1982年完成最初的資料蒐集[53]。最近的有2度視場星系紅移巡天,測量宇宙在一個部份的大尺度結構,量測了22萬個星系的z值,最後的結果已經在2003年6月釋出。[54][55](除了描繪星系在大尺度的模型,2度視場也可以估計微中子質量的上限。)其他值得重視的研究還有史隆數位巡天(SDSS),在2005年仍在繼續進行中,目標瞄準在觀測一億個天體[56]。SDSS已經觀測到紅移高達0.4的星系和紅移超過z = 6的類星體。深度2紅移巡天使用凱克望遠鏡和新的“DEIMOS”光譜儀,是深度1計劃的延續。深度2是設計來研究紅移0.7或更高的黯淡星系,因此可以填補SDSS和2df計劃的不足。[57]
來自物理的光學或輻射轉換的效應
在輻射轉移和物理光學的主題中會總結電磁輻射中波長和頻率轉換可能發生的現象和交互作用導致位移的結果。在這些情況下位移和物理上對應的能量轉移到物質或其他的光子,而不是歸結於參考座標系的轉變之間。這些轉移可以歸結於沃爾夫效應或是來自於基本粒子、微粒物質、或來自電介質的折射率的漲落,其導致電磁輻射的散射。[3][4][5]當這些現象對應於“紅移”或“藍移”的現象時,是物理的電磁輻射場本身的交互作用或是介入(干預)的物質來自參考座標系效應的現象。在天文物理,質-光交互作用的結果在輻射場的能量的遷移上通常是「紅化」(reddening)而不是「紅移」,而這個項目通常是保留在前面的效應中討論的。[3][4][5]
在許多情況下散射會導致輻射的紅化,因為熵會使光子趨向最低能量而減少高能的光子(總能量守恆)。[3][4][5]除了在小心控制的情況下,散射不會在同一個變化中橫跨整個光譜,換言之,任何一個波長上計算得到的z只是一個對應於波長的函數,而且,來自介質的隨機散射通常可能發生在任何的角度上,而z又是一個散射角的函數。如果多次的散射發生,或是散射的粒子在相對的運動中,那麼通常都會造成譜線的畸變。[3][4][5]
在恆星際天文學,可見光譜會因為穿過星際物質的散射過程出現星際紅化[3][4][5]:類似於在日出或日落時大氣層造成太陽光偏紅和天空是藍色的瑞利散射。這種明顯的轉移成紅色的現象,是因為譜線中的紅色部分沒有被轉移成其他的波長,以及額外的黯淡和畸變結合,這些現象使光子在視線中出現或消失。[o]
注释
^ 斯里弗一开始将其观测结果发表在一篇题为《仙女座星云的径向速度》(英语:The radial velocity of the Andromeda Nebula)[14]的文章中。在这篇文章中,他报告了于1912年9月17日进行的首次多普勒观测,他写道:“这一在迄今为止的观测数据中前所未有的速度令人怀疑其它的因素不足以引起这一类速位移。我相信目前也不会有其他能够解释它的方式。”三年后,在其发表在《大众天文学》(英语:Popular Astronomy)的一篇题为《星云的光谱观测》(英语:Spectrographic Observations of Nebulae)的文章中[15],他提出:“仙女座螺旋星云具有世所罕见的-300km/s的速度。这一早前的发现展示相关方法不仅可以用来研究螺旋星云的光谱还可以用来研究它们的速度。”斯里弗报告了15个遍布整个天球的螺旋星云的速度。除了三个之外,它们基本都具有“正”的速度(也就是退行速度)。
^ 这一点在20世纪30年代即被物理学家以及天文学家察觉到。亚瑟·爱丁顿爵士所著的《膨胀的宇宙:天文学“大争论”,1900-1931》(英语:The Expanding Universe: Astronomy's 'Great Debate', 1900-1931)是较早发行的一本细致描述相关话题的通俗读物。
^ NASA所属的雨燕卫星于2004年5月25日所探测到的情况即是一个例子[17]:“在伽马射线暴主脉冲附近获取的伽马射线谱由于缺少明显特征因而并不能作为红移的标志。然而对于伽马射线暴余晖的光学探测却可以得到具有明显谱线的光谱,其可以用来对红移进行精准测量。”
^ 其中z为紅移,v为速度,c为光速,γ为勞侖茲因子, a为宇宙標度因子,G为萬有引力常數,M为物體質量,r为史瓦西径向坐标。
^ 这种形式仅在不存在本动速度的宇宙中成立,否则红移应以下面这种形式合成:
- 1+z=(1+zDoppler)(1+zexpansion){displaystyle 1+z=(1+z_{mathrm {Doppler} })(1+z_{mathrm {expansion} })}
依照其得到的解,退行的物体会蓝移,趋近的物体则会红移[23]。
- 1+z=(1+zDoppler)(1+zexpansion){displaystyle 1+z=(1+z_{mathrm {Doppler} })(1+z_{mathrm {expansion} })}
^ 哈勃空间望远镜曾对5 Mpc外物体的本动速度进行观测,相关结果于2003年发表[25]。
^ 这是因为时空度规的膨胀可以通过广义相对论进行描述,并且是一种动态变化的度量,这与固定的闵可夫斯基度规相反。空间由于并非物质,所以可以不受光速上限的约束,膨胀速度可以比光速更快。
^ 這類似於傳統中由中心至觀測者的距離,但實際是史瓦西坐标。
^ 參考薩克斯-沃爾夫效應。
^ 在红移现象发现之初,弗里茨·兹威基曾提出“光线老化”假说来解释这一现象。虽然这一假说一般只在作为红移理论发展的一个节点时会被提及到,但在非标准宇宙学中,配合着内禀红移假说,其也能得到一定的实际应用。相关研究者曾对20世纪30年代之后正式发表过的多种红移现象替代理论进行过综述[33]。2001年,天文学家杰佛瑞·伯比奇在一篇评论中提出自20世纪60年代以来,相关讨论就已在天文学界日趋边缘化[34]。伯比奇与霍尔顿·阿尔普在研究类星体性质时曾尝试发展一种替代红移机制,但他们的同行大多对其不以为然。
^ 史隆數位巡天的研究人员曾对K修正做过讲解[38]。
^ 系外行星追踪器是采用这一技术的探测计划之一,其可以即时追踪多个目标的红移变化[39]。
^ 1871年,赫爾曼·卡爾·沃格爾测量了金星的自转速率。斯里弗在研究螺旋星云时也进行过类似观测。
^ 宇宙背景探测者对于宇宙微波背景辐射曾进行了精准的观测,最终发表的数值为2.73 K[44]。
^ 散射的過程請參考散射的條目。
參考資料
^ Feynman, R.; Leighton, R.; Sands, M. The Feynman Lectures on Physics. Vol. 1. Addison-Wesley. 1989. ISBN 978-0-201-51003-4 (英语).
^ Taylor, E. F.; Wheeler, J. A. Spacetime Physics: Introduction to Special Relativity(2nd ed.). W.H. Freeman. 1992. ISBN 978-0-7167-2327-1 (英语).
^ 3.03.13.23.33.43.53.63.73.83.9 Binney, J.; Merrifeld, M. Galactic Astronomy. Princeton University Press. 1998. ISBN 978-0-691-02565-0 (英语).
^ 4.04.14.24.34.44.54.64.74.84.9 Carroll, B. W.; Dale, A. O. An Introduction to Modern Astrophysics. Addison-Wesley Publishing Company, Inc. 1996. ISBN 978-0-201-54730-6 (英语).
^ 5.05.15.25.35.45.55.65.75.85.9 Kutner, M. Astronomy: A Physical Perspective. Cambridge University Press. 2003. ISBN 978-0-521-52927-3 (英语).
^ 6.06.16.2 Misner, C.; Thorne, K. S.; Wheeler, J. A. Gravitation. San Francisco: W. H. Freeman. 1973. ISBN 978-0-7167-0344-0 (英语).
^ 7.07.17.2 Weinberg, S. Gravitation and Cosmology. John Wiley. 1971. ISBN 978-0-471-92567-5 (英语).
^ Doppler, C. Beiträge zur fixsternenkunde. Prague: Druck von G. Haase sohne. 1846 (德语).
^ Maulik, D. Doppler sonography: A brief history. Doppler ultrasound in obstetrics and gynecology. Springer Berlin Heidelberg. 2005: 1–7 (英语).
^ O'Connor, J. J.; Robertson, E. F. Christian Andreas Doppler. MacTutor. 1998 [2016-07-10] (英语).
^ 11.011.1 Huggins, W. Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II., 1868. Philosophical Transactions of the Royal Society of London. 1868, 158: 529–564 (英语).
^ Reber, G. Intergalactic Plasma. Astrophysics and Space Science. 1995, 227: 93–96 (英语).
^ Bélopolsky, A. On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle. Astrophysical Journal. 1901, 13: 15 (英语).
^ Slipher, V. M. The radial velocity of the Andromeda Nebula. Lowell Observatory Bulletin. 1913, 2: 56–57 (英语).
^ Slipher, V. M. Spectrographic observations of nebulae. Popular Astronomy. 1915, 23: 21–24 (英语).
^ Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proceedings of the National Academy of Sciences. 1929, 15 (3): 168–173 (英语).
^ Swift Redshift Measurements. NASA. 2012 [2016-07-10] (英语).
^ Ives, H. E.; Stilwell, G. R. An experimental study of the rate of a moving atomic clock. JOSA. 1938, 28 (7): 215–219 (英语).
^ Freund, J. Special Relativity for Beginners. World Scientific. 2008: 120. ISBN 981-277-160-3 (英语).
^ Ditchburn, R. Light. Dover. 1961: 329. ISBN 0-12-218101-8.
^ Eddington, A. The Expanding Universe: Astronomy's 'Great Debate', 1900-1931. Cambridge University Press. 1933. ISBN 0521349761 (英语).
^ Harrison, E. R. Cosmology: The Science of the Universe. New York: Cambridge University Press. 1981. ISBN 978-0521661485 (英语).
^ Davis, T. M.; Lineweaver, C. H.; Webb, J. K. Solutions to the tethered galaxy problem in an expanding universe and the observation of receding blueshifted objects. American Journal of Physics. 2003, 71: 358–364 (英语).
^ 24.024.124.2 Peebles, P. J. E. Principles of Physical Cosmology. Princeton University Press. 1993. ISBN 978-0-691-01933-8 (英语).
^ Karachentsev, I. D.; et al. Local galaxy flows within 5 Mpc. Astronomy & Astrophysics. 2003, 398 (2): 479–491 (英语). 引文使用过时参数coauthor (帮助)
^ Harrison, E. The redshift-distance and velocity-distance laws. The Astrophysical Journal. 1993, 403 (1): 28–31 (英语).
^ Odenwald, S.; Fienberg, R. T. Galaxy redshifts reconsidered (PDF). Sky and Telescope. 1993, 85 (2): 31–35. (原始内容 (PDF)存档于2016-08-17) (英语).
^ Weiss, M. What Causes the Hubble Redshift. The Original Usenet Physics FAQ. 1994 [2016-07-07] (英语).
^ Chant, C. A. Notes and Queries (Telescopes and Observatory Equipment-The Einstein Shift of Solar Lines). Journal of the Royal Astronomical Society of Canada. 1930, 24: 390 (英语).
^ Einstein, A. On the relativity principle and the conclusions drawn from it. Jahrbuch der Radioaktivität und Elektronik. 1907, 4: 411–462 (德语).
^ Pound, R. V.; Rebka Jr., G. A. Apparent weight of photons. Physical Review Letters. 1960, 4 (7): 337 (英语).
^ Sachs, R. K.; Wolfe, A. M. Perturbations of a cosmological model and angular variations of the cosmic microwave background. Astrophysical Journal. 1967, 147 (1): 73–90 (英语).
^ Reboul, H. J. Untrivial redshifts-A bibliographical catalogue. Astronomy and Astrophysics Supplement Series. 1981, 45: 129–144 (英语).
^ Burbidge, G. Noncosmological redshifts. Publications of the Astronomical Society of the Pacific. 2001, 113 (786): 899–902 (英语).
^ Budding, E. Introduction to Astronomical Photometry. Cambridge University Press. 1993. ISBN 978-0-521-41867-6 (英语).
^ Baum, W. A. Problems of extra-galactic research. (编) G. C. McVittie. IAU Symposium No. 15. Kluwer: 390. 1962 (英语).
^ Bolzonella, M.; Miralles, J.-M.; Pelló, R. Photometric Redshifts based on standard SED fitting
procedures. 2000. arXiv:http://arxiv.org/pdf/astro-ph/0003380.pdf 请检查|arxiv=值 (帮助) [astro-ph] (英语). 参数|title=值左起第52位存在換行符 (帮助); 不支持的参数使用了arXiv (帮助)
^ Hogg, D. W.; Baldry, I. K.; Blanton, M. R.; Eisenstein, D. J. The K correction. arXiv:http://arxiv.org/pdf/astro-ph/0210394v1 请检查|arxiv=值 (帮助) [astro-ph] (英语). 不支持的参数使用了arXiv (帮助)
^ Ge, Jian; et al. The First Extrasolar Planet Discovered with a New-Generation High-Throughput Doppler Instrument. The Astrophysical Journal. 2006, 648 (1): 683–695 (英语). 引文使用过时参数coauthor (帮助)
^ Libbrecht, K. G. Solar and stellar seismology. Space Science Reviews. 1988, 37 (3-4): 275–301 (英语).
^ Oort, J. H. The formation of galaxies and the origin of the high-velocity hydrogen. Astronomy and Astrophysics. 1970, 7: 381–404 (英语).
^ Asaoka, Ikuko. X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole (PDF). Astronomical Society of Japan, Publications. 1989, 41 (4): 763–778. ISSN 0004-6264 (英语).
^ Rybicki, G. B.; Lightman, A. R. Radiative Processes in Astrophysics. John Wiley & Sons. 1979: 288. ISBN 978-0-471-82759-7 (英语).
^ Fixsen, D. J.; et al. Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument. Astrophysical Journal. 1994, 420: 445 (英语). 引文使用过时参数coauthor (帮助)
^ Fan, Xiahoui; et al. A Survey of z>5.7 Quasars in the Sloan Digital Sky Survey. II. Discovery of Three Additional Quasars at z>6. The Astronomical Journal. 2003, 125 (4): 1649–1659 (英语). 引文使用过时参数coauthor (帮助)
^ Egami, E.; et al. Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218. The Astrophysical Journal. 2005, 618 (1): L5–L8 (英语). 引文使用过时参数coauthor (帮助)
^ Pelló, R.; Schaerer, D.; Richard, J.; Le Borgne, J.-F.; Kneib, J. P. ISAAC/VLT observations of a lensed galaxy at z = 10.0. Astronomy and Astrophysics. 2004, 416: L35 (英语).
^ Binney, James; and Scott Treimane. Galactic dynamics. Princeton University Press. ISBN 978-0-691-08445-9 (英语). 引文使用过时参数coauthors (帮助)
^ Peebles, P. J. E.; Ratra, Bharat. The cosmological constant and dark energy. Reviews of Modern Physics. 2003, 75: 559–606 (英语).
^ Permutter, S.; et al. (The Supernova Cosmology Project). Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophysical J. 1999, 517: 565–86 (英语). 引文使用过时参数coauthor (帮助)
^ Riess, A. G.; et al. (Supernova Search Team). Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astronomical J. 1998, 116: 1009–38 (英语). 引文使用过时参数coauthor (帮助)
^ Geller, M. J.; Huchra, J. P. Mapping the Universe. Science. 1989, 246 (4932): 897–903 (英语).
^ THE CfA REDSHIFT SURVEY. [2016-07-10] (英语).
^ Cole, S.; et al. The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications. Mon. Not. Roy. Astron. Soc. 2005, 362 (2): 505–34. Bibcode:2005MNRAS.362..505C. arXiv:astro-ph/0501174. doi:10.1111/j.1365-2966.2005.09318.x (英语). 引文使用过时参数coauthor (帮助)
^ 2dF Galaxy Redshift Survey homepage. [2016-07-07] (英语).
^ The Sloan Digital Sky Survey: Mapping the Universe. [2016-07-10] (英语).
^ Davis, M.; DEEP2 collaboration. Science objectives and early results of the DEEP2 redshift survey. Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002. 2002. arXiv:astro-ph/0209419 (英语). 引文使用过时参数coauthor (帮助)
延伸阅读
Lineweaver, C. H.; Davis, T. M. Misconceptions about the big bang (PDF). Scientific American. 2005, 292 (3): 36–45 (英语).
外部連結
维基共享资源中相关的多媒体资源:紅移 |
内德·赖特对红移所做的讲解(英文)
迈克·路西乌克对红移所做的讲解(英文)
- 由美国红外处理和分析中心提供的对于红移的讲解(英文)
相關條目
- 蓝移
- 多普勒效應
- 重力紅移
- 类星体
- 哈伯定律
- 宇宙大爆炸理论
| ||||||||||||||||||||||||||||||||||||||||||
|






