Rearuh

平抛运动

曲线运动是指运动轨迹为曲线的运动。当物体运动的的速度与其所受到的合外力不在同一直线上的时候，物体便做曲线运动。典型的曲线运动有：平抛运动、斜抛运动、圆周运动等。勻速運動也是一種曲線運動。

速度的方向

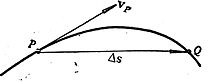
如图，设质点沿所示曲线运动，在某一时刻质点位于P{displaystyle P}点，经过Δt{displaystyle Delta t}时间后，质点移动到Q{displaystyle Q}点，它的位移为Δs{displaystyle Delta s}则质点在这段时间内的平均速度为v=ΔsΔt{displaystyle v={frac {Delta s}{Delta t}}}。^[1]当Δt{displaystyle Delta t}趋近于0时，则Q{displaystyle Q}点趋近于P{displaystyle P}点，Δs{displaystyle Delta s}的方向就趋近于路径上P{displaystyle P}点的方向，由即时速度的定义可知：P{displaystyle P}点的切线方向，就是质点在P{displaystyle P}的即时速度方向。由此得出：在曲线运动中，质点在某点的速度的方向就是该点的切线方向（指向前进一侧）。

曲线运动是变速运动，速度的大小和方向都在变化。做曲线运动的物体的瞬时速度定义为：

v=dsdt{displaystyle v={frac {ds}{dt}}}

方向是该点轨迹的切线方向。^[2]

物体的瞬时加速度定义为：

a=dvdt{displaystyle a={frac {dv}{dt}}}

因为速度方向随时间变化，所以做曲线运动的物体，加速度和速度一定不在同一直线上。当速度和加速度在同一直线上时，物体做直线运动；当速度和加速度垂直时，物体做匀速圆周运动。^[1]

下面讨论两种常见的曲线运动：平抛运动与匀速圆周运动。

平抛运动

枪炮、火箭等从一个位置抛出去的物体做的运动为抛体运动。若抛出去的物体初速度是水平方向的，这种抛体运动叫平抛运动。根据运动叠加原理（一个运动可以看成几个同时进行的各自独立的运动的叠加。）可以发现，在忽略空气阻力时，可以看作是水平方向上的匀速运动与竖直方向上的自由落体运动的叠加。若在竖直平面上建立直角坐标系xOy{displaystyle xOy},则物体在任一时刻t{displaystyle t}的水平速度vx{displaystyle v_{x}}和数值方向上的速度vy{displaystyle v_{y}}分别为：

{vx=v0vy=gt{displaystyle {begin{cases}v_{x}=v_{0}\v_{y}=gtend{cases}}}

物体在t{displaystyle t}时间内水平方向的位移和竖直方向的位移分别为：

{x=v0ty=12gt2{displaystyle {begin{cases}x=v_{0}t\y={tfrac {1}{2}}gt^{2}end{cases}}}

由于速度、位移都是矢量，所以，物体在t{displaystyle t}时刻的合速度为v=vx+vy{displaystyle v=v_{x}+v_{y}}及t{displaystyle t}时刻内的合位移s=x+y{displaystyle s=x+y}均可由平行四边形法则求得，如图所示，上文提到的位移公式可得：y=12gx2v22=g2v02⋅x2{displaystyle y={frac {1}{2}}g{frac {x^{2}}{v_{2}^{2}}}={frac {g}{2v_{0}^{2}}}cdot x^{2}}。这就是平抛运动的标准运动方程。

等速率圆周運動

定义：如果质点沿圆周運動的速度不变，即在任意时间间隔内所通过的弧长相等，这种运动叫做等速率圆周運動。

由此可见，等速率圆周運動的速度方向不断改变，所以等速率圆周運動不是等速運動。因为质点做匀速圆周运动时，每经过一段时间，物体就绕圆周运动一圈，所以匀速圆周运动是一种周期性运动。物体绕圆周运动一圈的时间叫做周期，在单位时间内运行的周期数称为频率。在物体作匀速圆周运动时的线速度由以下公式计算：

v=2πRT{displaystyle v={frac {2pi R}{T}}} 或 v=2πRf{displaystyle v=2pi Rf} （R{displaystyle R}：圆的直径 T{displaystyle T}：周期 f{displaystyle f}：频率）

向心力：要使物体作等速率圆周運動，必须时时刻刻给物体一个与线速度方向垂直，沿着半径指向圆心的力，这个力稱為向心力。物体的运动方向不断改变就是因为向心力的作用。

向心力是物体作等速率圆周運動的必要条件之一（另一个必要条件是物体必须具有一定的切線速率）只有满足这两个条件，物体才能做等速率圆周運動。

向心力的大小满足下列公式：

F=mv2R{displaystyle F=m{frac {v^{2}}{R}}}

向心加速度：由向心力产生的加速度叫做向心加速度，它的方向也是指向圆心的。根据牛顿第二定律

动力学描述

做曲线运动的物体在其运动轨迹的切向（沿速度方向）和法向（垂直于速度方向）均受力。在这两个方向上，都满足牛顿第二定律。

切向

Fτ=mdvdt=maτ{displaystyle F_{tau }=m{frac {dv}{dt}}=ma_{tau }}

Fτ{displaystyle F_{tau }}是物体在沿速度方向受到的分力，aτ{displaystyle a_{tau }}为物体在此方向的加速度。这个加速度改变物体速度的大小。^[3]

法向

在垂直于速度的方向上：
Fn=man=mv2ρ{displaystyle F_{n}=ma_{n}=m{frac {v^{2}}{rho }}}

Fn{displaystyle F_{n}}即为物体收到的法向力（在圆周运动中，此力就是向心力），v{displaystyle v}是这一时刻物体的速度，ρ{displaystyle rho }是物体的运动轨迹上，物体所处的这一点的曲率半径。

法向力改变物体的速度方向，而不改变其大小。^[3]

等加速曲线运动

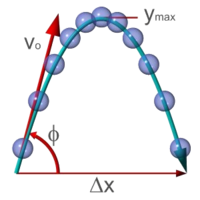
如果一个物体不是垂直向上发射，而是与地平面呈Φ{displaystyle Phi }角度射出，那麼，这物体会按照抛物线軌跡移动，它的水平运动与垂直运动可以各自独立计算。假设，这物体是以最初速率v0=50m/s{displaystyle v_{0}=50m/s}，与地平面呈Φ=30∘{displaystyle Phi =30^{circ }}角度射出。

请问在碰到地面以前，它会在空中飞行多远？

垂直方向，这物体会感觉到−9.81m/s2{displaystyle -9.81m/s^{2}}加速度；水平方向，不会感觉到有任何加速度。所以，水平位移是

Δx=xf−xi=vicos⁡(Φ) t+12at2=vicos⁡(Φ) t{displaystyle Delta x=x_{f}-x_{i}=v_{i}cos(Phi ) t+{frac {1}{2}}at^{2}=v_{i}cos(Phi ) t}

为要解答这问题，必须找到t{displaystyle t}值。这是可以做到的，只需分析垂直的运动。假设垂直位移为零，用类似前面直线运动的方法来找t{displaystyle t}值：

0=visin⁡(Φ) t+12at2=t(visin⁡(Φ)+12at){displaystyle 0=v_{i}sin(Phi ) t+{frac {1}{2}}at^{2}=t(v_{i}sin(Phi )+{frac {1}{2}}at)}

现在求解t{displaystyle t}的表達式，代入原先的水平位移方程式。

Δx=vicos⁡(Φ)(−2visin⁡(Φ)a)=−vi2sin⁡2(Φ)a=220.70 m{displaystyle Delta x=v_{i}cos(Phi )left({frac {-2v_{i}sin(Phi )}{a}}right)=-{frac {v_{i}^{2}sin 2(Phi )}{a}}=220.70 m}

参见

• 平移运动


• 匀速运动


• 平抛运动


• 简谐运动


• 匀速圆周运动


• 斜抛运动

参考资料

• 物理（必修2），人民教育出版社