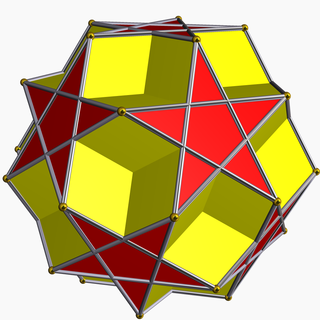
Dodecadodecahedron
| Dodecadodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 24, E = 60 V = 30 (χ = −6) |
| Faces by sides | 12{5}+12{5/2} |
| Wythoff symbol | 2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U36, C45, W73 |
| Dual polyhedron | Medial rhombic triacontahedron |
| Vertex figure |  5.5/2.5.5/2 |
| Bowers acronym | Did |
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).
The edges of this model form 10 central hexagons, and projected onto a sphere, represent 10 great circles. These 10, along with the great circles from projections of two other polyhedra, form the 31 great circles of the spherical icosahedron used in construction of geodesic domes.
Contents
1 Wythoff constructions
2 Net
3 Related polyhedra
3.1 Medial rhombic triacontahedron
3.1.1 Stellation
3.1.2 Related hyperbolic tiling
4 See also
5 References
6 External links
Wythoff constructions
It has four Wythoff constructions between four Schwarz triangle families: 2 | 5 5/2, 2 | 5 5/3, 2 | 5/2 5/4, 2 | 5/3 5/4, but represent identical results. Similarly it can be given four extended Schläfli symbols: r{5/2,5}, r{5/3,5}, r{5/2,5/4}, and r{5/3,5/4} or as Coxeter-Dynkin diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and
, and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Net
A shape with the same exterior appearance as the dodecadodecahedron can be constructed by folding up these nets:

12 pentagrams and 20 rhombic clusters are necessary. However, this construction replaces the crossing pentagonal faces of the dodecadodecahedron with non-crossing sets of rhombi, so it does not produce the same internal structure.
Related polyhedra
Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the small dodecahemicosahedron (having the pentagrammic faces in common), and with the great dodecahemicosahedron (having the pentagonal faces in common).
 Dodecadodecahedron |  Small dodecahemicosahedron |
 Great dodecahemicosahedron |  Icosidodecahedron (convex hull) |

Animated truncation sequence from {5/2, 5} to {5, 5/2}
This polyhedron can be considered a rectified great dodecahedron. It is center of a truncation sequence between a small stellated dodecahedron and great dodecahedron:
The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams). The truncation of the dodecadodecahedron itself is not uniform and attempting to make it uniform results in a degenerate polyhedron (that looks like a small rhombidodecahedron with {10/2} polygons filling up the dodecahedral set of holes), but it has a uniform quasitruncation, the truncated dodecadodecahedron.
| Name | Small stellated dodecahedron | Truncated small stellated dodecahedron | Dodecadodecahedron | Truncated great dodecahedron | Great dodecahedron |
|---|---|---|---|---|---|
Coxeter-Dynkin diagram | |||||
| Picture |  |  |  |  |  |
It is topologically equivalent to a quotient space of the hyperbolic order-4 pentagonal tiling, by distorting the pentagrams back into regular pentagons. As such, it is topologically a regular polyhedron of index two:[1][2]

The colours in the above image correspond to the red pentagrams and yellow pentagons of the dodecadodecahedron at the top of this article.
Medial rhombic triacontahedron
| Medial rhombic triacontahedron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 30, E = 60 V = 24 (χ = −6) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU36 |
| dual polyhedron | Dodecadodecahedron |
The medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the dodecadodecahedron. It has 30 intersecting rhombic faces.
It can also be called the small stellated triacontahedron.
Stellation
The medial rhombic triacontahedron is a stellation of the rhombic triacontahedron, which is the dual of the icosidodecahedron, the convex hull of the dodecadodecahedron (dual to the original medial rhombic triacontahedron).
Related hyperbolic tiling
It is topologically equivalent to a quotient space of the hyperbolic order-5 square tiling, by distorting the rhombi into squares. As such, it is topologically a regular polyhedron of index two:[3]

Note that the order-5 square tiling is dual to the order-4 pentagonal tiling, and a quotient space of the order-4 pentagonal tiling is topologically equivalent to the dual of the medial rhombic triacontahedron, the dodecadodecahedron.
See also
- List of uniform polyhedra
References
^ The Regular Polyhedra (of index two), David A. Richter
^ The Golay Code on the Dodecadodecahedron, David A. Richter
^ The Regular Polyhedra (of index two), David A. Richter
Badoureau (1881), "Mémoire sur les figures isoscèles", journal de l´École Polytechnique, 49: 47–172.mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
Hess, Edmund (1878), Vier archimedeische Polyeder höherer Art, Cassel. Th. Kay, JFM 10.0346.03
Pitsch (1882), "Über halbreguläre Sternpolyheder", Zeitschrift für das Realschulwesen, 7, JFM 14.0448.01
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208
External links
- Weisstein, Eric W. "Dodecadodecahedron". MathWorld.
- Weisstein, Eric W. "Medial Rhombic Triacontahedron". MathWorld.
- Uniform polyhedra and duals